Алгоритм деления

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, с нулями, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

Методика обучения детей делению столбиком

Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.

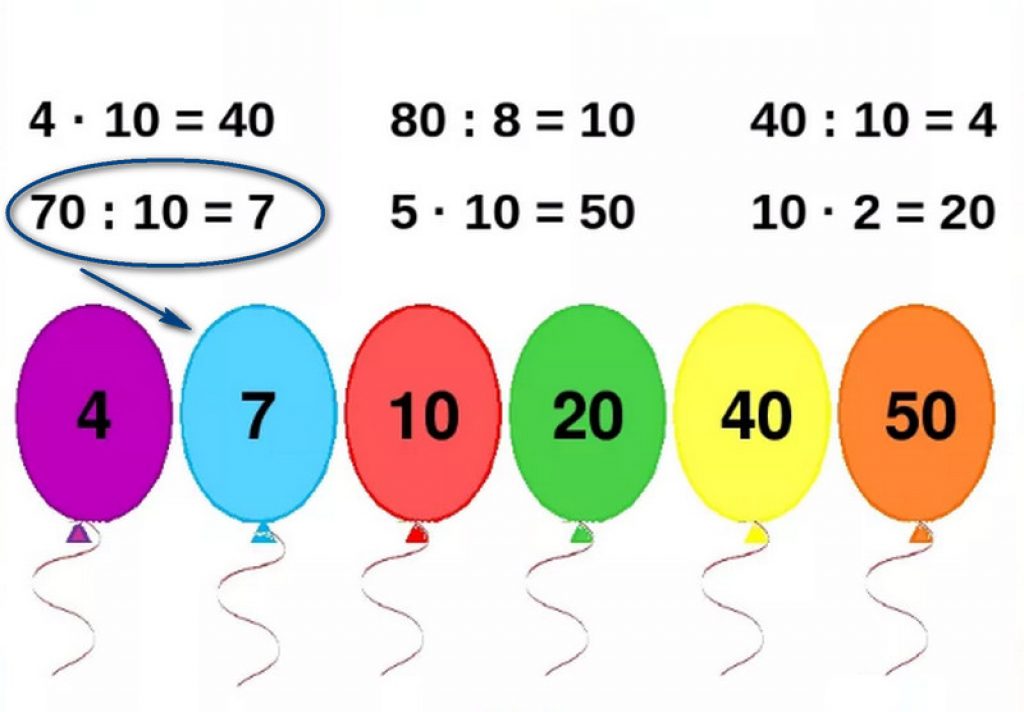
Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).

Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.

Наглядный пример для ученика и родителей

Деление в столбик можно наглядно объяснить на этом примере.

1. Записывают в столбик 2 числа: делимое – 536 и делитель – 4.
2. Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
3. 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 – 4.
4. Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
5. К единице сносится следующее разрядное число – 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 – в частное, как следующее разрядное число.
6. Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число – 6.
7. 16 снова делится на 4. В ответ записывают 4, а в столбик деления – 16, подводят черту и в разнице 0.

Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

Деление натуральных чисел с остатком. Проверка результата

Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.

На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.

Важно!

Остаток всегда меньше делителя!

На втором этапе проверяется справедливость равенства a=b·c+d. Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.

Пример 6. Проверка результата деления натуральных чисел с остатком. 

Проверим, верно ли, что 506÷28=17 (остаток 30).

Сравниваем остаток и делитель: 30>28.

Значит, деление выполнено неверно.

Пример 7. Проверка результата деления натуральных чисел с остатком. 

Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5. Правильно ли он сделал?

Чтобы узнать это, сначала сравниваем остаток и делитель: 5<13.

Первый пункт проверки пройден, переходим ко второму.

Запишем формулу a=b·c+d. a=121; b=13; c=9; d=5.

Подставляем значения и сравниваем результаты

13·9+5=117+5=122; 121≠122

Значит, в вычисления школьника где-то закралась ошибка.

Пример 8. Проверка результата деления натуральных чисел с остатком. 

Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111. В результате у него получилось число 54 с остатком 4. Все ли правильно посчитано?

Проверим! Остаток 4 меньше, чем делитель 111, поэтому переходим ко второму этапу проверки.

Используем формулу a=b·c+d, где a=5998; b=111; c=54; d=4.

После подстановки, имеем:

5998=111·54+4=5994+4=5998.

Равенство корректно, а значит, и деление выполнено верно.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Деление повторным вычитанием [ править ]

Простейший алгоритм деления, исторически включенный в алгоритм наибольшего общего делителя , представленный в ЭлементахЕвклида , Книга VII, Предложение 1, находит остаток при двух положительных целых числах, используя только вычитания и сравнения:

Доказательство того, что частное и остаток существуют и уникальны (описано в евклидовом делении ), дает начало алгоритму полного деления с использованием сложений, вычитаний и сравнений:

Эта процедура всегда дает R ≥ 0. Хотя она очень проста, она требует Ω (Q) шагов, поэтому она экспоненциально медленнее, чем даже алгоритмы медленного деления, такие как деление в столбик. Это полезно, если известно, что Q невелик (является алгоритмом, чувствительным к выходу ) и может служить исполняемой спецификацией.

Обучение делению с остатком

Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:

• Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
• Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
• Запишите под числом 35 число 32.
• Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.

Простые примеры для ребенка

На этом же примере можно продолжить:

• При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
• При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
• Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
• В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
• При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.

Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.

Что нужно знать, что бы научиться делить

Прежде, чем приступить к делению, нужно убедиться в том, что ребенок усвоил азы математики – сложение, вычитание.

Надо объяснить ему основы умножения и проверить знание таблицы умножения. Необходимо убедиться, как он выучил разряды чисел.

Без этих основ вряд ли получится проводить арифметические операции с числами

Математика не терпит пробелов в знаниях, поэтому важно вложить этот принцип в голову ребенка с раннего возраста. Даже если какая-то часть материала была пропущена по причине болезни или иного отсутствия на уроке, материал должен быть выучен

Пробелы в знаниях повлекут за собой трудности в решении задач, примеров, а в старших классах и проблемы в изучении других дисциплин.

Проверка результата деления

Проверка никогда не бывает лишней, особенно, если мы делили большие числа. Как проверять, правильно ли выполнено деление натуральных чисел? При помощи умножения!

Проверка результата деления

Чтобы проверить правильно ли выполнено деление, нужно частное умножить на делитель. В результате должно получится делимое.

Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.

Смысл этого действия очень прост. Например, у нас было a предметов, и эти a предметов мы разложили на b кучек. В каждой кучке оказалось по с предметов. Математически это выглядит так:

a÷b=c.

Теперь объединим обратно все b кучек по с предметов. В результате должно получится та же совокупность предметов a.

b·c=a.

Рассмотрим проведение проверки на двух примерах.

Пример 15. Проверка результата деления натуральных чисел

Число 475 разделили на 19. В результате получилось 25. Правильно ли выполнено деление?

Умножим частное 25 на делитель 19 и выясним, верно ли разделили числа.

25·19=475.

Число 475 равно делимому, значит, деление выполнено верно.

Пример 16. Проверка результата деления натуральных чисел

Разделите и проверьте результат:

1024÷32=?

Будем представлять делимое в виде суммы слагаемых и осуществлять деление.

1024÷32=960+64÷32=960÷32+64÷32=30+2=32.

Проверим результат:

32·32=1024.

Вывод: деление выполнено верно.

Умножение и деление круглых чисел

Обратите внимание: круглым называется число, которое оканчивается нулем — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Круглые числа похожи на десятки

Разряд единиц круглых десятков равняется нулю.

Прочитайте таблицу круглых чисел:

Умножение и деление круглого двухзначного числа на однозначное выполняется по определенным правилам. Познакомьтесь с этими правилами.

Деление круглых чисел

Рассмотрим пример внетабличного деления:

В примерах деления круглого числа делим количество десятков и дописываем в ответе нуль.

Делим на 10 — убираем в ответе нуль.

В частном не пишем нули, если делимое, делитель — круглые числа.

Умножение круглых чисел

А знаете ли вы, что за тысячелетия развития математики было придумано много вариантов умножения. Считалось, что для овладения искусством вычисление нужен талант. Итальянский математик 15 века Лука Пачоли  приводит 8 способов. Познакомимся с некоторыми из них.

Рассмотрите прием внетабличного умножения.

Двадцать умножить на три равно шестидесяти.

Воспользуемся правилом перестановки множителей, получим пример, который умеем решать.

Прочитайте правило внимательно.

При умножении круглого числа на однозначное, надо умножить десятки на второй множитель, в ответ справа добавить нуль.

Увеличить в десять раз — это значит написать в значение произведения первый множитель и добавить к нему 0 справа.

Произведение семи и десяти равно семидесяти.

Воспользуйтесь правилами математики внетабличного умножения и деления для решения примеров:

Проверьте:

Ошибок нет, молодцы. Ваша первая награда — красная ленточка.

Впереди ждут новые открытия, не отставайте, думайте, решайте.

Решение задач на движение в противоположных направлениях

Мы с вами на предыдущем уроке уже познакомились с величинами, которые встречаются в задачах на движение. Давайте вспомним ключевые формулы!

Сегодня нам  встретится  новое понятие «скорость удаления». Что это такое?

Например, от автобусной остановки отъехали в разных направлениях Дима на велосипеде и Валера на мотоцикле. Скорость Димы – 10 км/ч,  а Валеры –  50 км/ч. Скорость удаления 10 + 50 = 60 км/ч.

Решим вместе задачу.

Задача

Улитки Бэлла и Элла ползли по одной дорожке в разных направлениях. Одна – на юг, другая – на север. Скорость движения Бэллы – 5 м/мин, а скорость движения Эллы – 7 м/мин. Через сколько минут расстояние между улитками будет 120 м?

Найдем скорость удаления двух улиток.

5 + 7 = 12 (м/мин)

Найдем время, зная расстояние 120 м и скорость 12 м/мин.

t= S v

120 : 12 = 10 (мин)

Ответ: 10 минут

Решение можно записать выражением 120 : (5 + 7) = 10

Решим задачу, обратную данной. Пусть время 10 минут будет известно, расстояние, которое преодолели улитки – 120 м. Скорость Бэллы – 5 м/мин. А вот скорость Эллы нам нужно найти.

Зная расстояние и время, найдем скорость удаления улиток.

v = St

120 : 10 = 12 (м/мин)

Найдем скорость Эллы.

12 – 5 = 7 (м/мин)

Ответ: 7 м/мин

Решение задачи можно записать в виде выражения (120 : 10) – 5 = 7

Следующую задачу решите самостоятельно. Внимательно рассмотрите схематический рисунок.

Красный и зеленый автомобили выехали в противоположных направлениях. Скорость красного автомобиля – 60 км/м, а зеленого – 40 км/м. Через некоторое время расстояние между красной и зеленой машинами стало 500 км. Найди это время.

Проверь себя.

60 + 40 = 100 (км/ч) – скорость удаления красной и зеленой машин.

500 : 100 = 5 (ч) – будут в пути.

Ответ: 5 часов.

Решение можно записать в виде выражения 500 : (60 + 40) = 5

Сегодня на уроке мы научились умножать и делить на числа, оканчивающиеся нулями, познакомились с правилом деления с остатком, узнали новое понятие «скорость удаления».

Как объяснить ребенку, что такое умножение и деление

Причина непонимания умножения и деления в большинстве случаев кроется в банальном отсутствии внимательности у школьника

В раннем возрасте деткам сложно концентрировать внимание на чем-то конкретном более 15 минут, поэтому они поддаются влиянию различных отвлекающих факторов

Обратите внимание! Ребенок может стесняться задавать учителю один и тот же вопрос несколько раз, потому что боится показаться глупым в глазах окружающих. В такой ситуации нужно провести со школьником беседу, уточнить детали, которые ему непонятны после объяснения материала, и успокоить

Для того чтобы объяснить ребенку понятие «умножение», для начала нужно подготовить распечатку таблицы умножения Пифагора (нарисовать ее собственноручно или распечатать на принтере). Без такой таблицы не получится разъяснить сам принцип только с помощью обычных примеров. На начальном этапе пусть ребенок сам постарается определить закономерность (желательно, чтобы это занятие стало увлекательной игрой).

Изучая данный раздел математики, детишкам должны быть известны такие простые действия, как сложение и вычитание. Разъясняя своему чаду принцип работы умножения, рекомендуется использовать самый элементарный прием. Нужно разобраться, что фраза «умножить число шесть на число два» или же «шестью два» означает то же самое, что и «шесть плюс шесть». Также следует записать пример в виде цифр для визуализации: 6*2 = 6+6.

Таблица умножения Пифагора

Объяснение принципа деления

Для того чтобы разъяснить ребенку, как нужно правильно делить, совсем необязательно использовать скучные учебники. Вместо них можно взять яблоки, конфеты и игрушки. Взрослый должен попросить карапуза разделить между тремя – четырьмя куклами пять конфеток или яблок, а далее количество фруктов следует постепенно увеличивать до 8-10.

Важно! Малыш сначала будет раскладывать предметы медленно, делая большие паузы, но кричать на него категорически запрещено, лучше запастись терпением. После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог

Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну»

После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог. Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну».

Еще один игровой пример представлен делением на цифрах. Нужно сказать карапузу, что цифры – это те же фрукты или конфеты и приучать, что количество сладостей, которые следует разделить, принято называть «делимое». А люди, на которых делятся конфеты, – это «делитель».

Обучение делению в столбик в форме игры

Можно поставить задачи таким образом:

1Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.

2Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.

3Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.

4Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.

Деление чисел

Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.

Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Как делить в столбик с остатком?

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Деление с остатком

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

слайд из презентации о делении чисел с остатком

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Решим пример \(\textcolor{red} {295383\div 34}\).

Далее записываем известные
компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor{red} {8\cdot 37=272}\). Записываем его под 295 и находим разницу: \(\textcolor{red} {295-272=23}\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия \(\textcolor{red} {295383\div 34=8687}\) и 25 в остатке.

Рассмотрим еще один пример. \(\textcolor{red} {25326\div 63}\).

Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.

Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать , поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.

Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.

126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления \(\textcolor{red} {25326\div 63=402}\).

Итак, в общем виде алгоритм деления в столбик выглядит так:1. Находим первое неполное делимое и количество цифр в частном.2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.4. Ставим между ними знак минус и выполняем действие.5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.7. Если неполное делимое невозможно разделить на делитель, то в частном ставится и к этому неполному делимому сносится следующая цифра.

Как научить ребенка делению в форме игры

Скучные учебники лучше отложить в сторону на время. Малыш быстро усвоит сложный материал, если мама или папа превратит обучение в интересную игру. Итак, как научить ребенка делению?

Для этого применяют упражнение:

1. Для проведения домашних занятий следует запастись конфетами или яблоками. Также понадобятся игрушки, с которыми любит возиться ученик. Нужно попросить малыша, чтобы он разделил четыре яблока или конфеты между двумя-тремя мишками или куклами. Затем количество предметов, подлежащих делению, увеличивается до шести, восьми, десяти.
2. Итак, игрушки «получили» конфеты или яблоки. Теперь ученик должен посчитать, сколько досталось каждому мишке или кукле. Обязательно следует подвести итог. Предположим, что игрушек было три и между ними были разделены шесть конфет. Следовательно, каждая «получила» по две. Нужно объяснить ребенку, что «разделить» означает всем раздать поровну.
3. Как научить ребенка делению дома? Для лучшего усвоения материала стоит изменить условия задачи. К примеру, нужно дать малышу шесть яблок и попросить распределить их между бабушкой, дедушкой и кошкой поровну. Затем это же количество предметов следует предложить ему поделить между бабушкой и животным. Обязательно следует объяснить ученику, почему результат оказался разным.