Как умножать в столбик

Что это такое?

Как объяснить ребенку умножение столбиком?

Как объяснить ребенку умножение столбиком?

Научить ребенка умножению — это реальная задача, но придется запастись терпением. Занятие должны быть регулярными, ведь только система поможет добиться желаемых результатов.

• Расскажите ребенку, что умножение — это повторение, сложение одинаковых чисел
• Напишите на листе бумаги примеры: 2+2+2+2+2 и 2х5
• Сделайте вместе с ребенком сравнение, как быстрее подсчитать сложением или умножением
• Чтобы закрепить эту полученную информацию, приведите примеры из жизни, но они должны быть не выдуманными. Например, к ребенку в гости идут 7 друзей. Для них готово лакомство — по 2 конфеты. Как быстрее подсчитать — сложением или умножением? Подсчитайте вместе с малышом и запишите на бумаге в виде примера: 7х2=14

Когда пройдет несколько занятий, таблица умножения будет выучена, тогда можно начинать объяснять ребенку умножение столбиком двухзначных и трехзначных чисел.

Умножение и деление круглых чисел

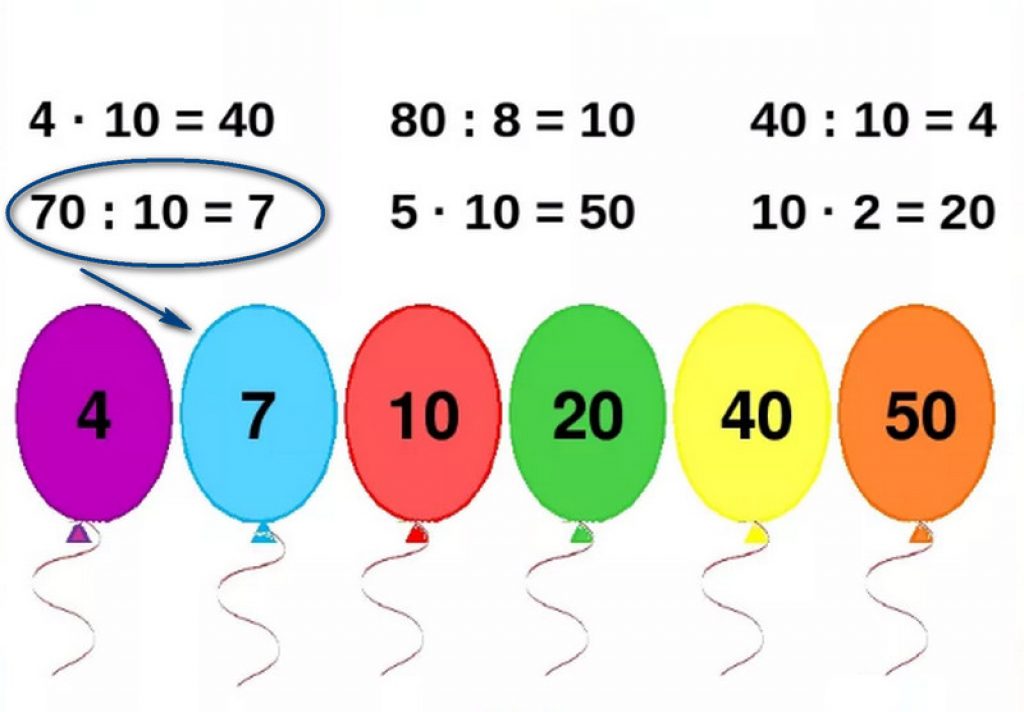
Обратите внимание: круглым называется число, которое оканчивается нулем — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Круглые числа похожи на десятки

Разряд единиц круглых десятков равняется нулю.

Прочитайте таблицу круглых чисел:

Умножение и деление круглого двухзначного числа на однозначное выполняется по определенным правилам. Познакомьтесь с этими правилами.

Деление круглых чисел

Рассмотрим пример внетабличного деления:

В примерах деления круглого числа делим количество десятков и дописываем в ответе нуль.

Делим на 10 — убираем в ответе нуль.

В частном не пишем нули, если делимое, делитель — круглые числа.

Умножение круглых чисел

А знаете ли вы, что за тысячелетия развития математики было придумано много вариантов умножения. Считалось, что для овладения искусством вычисление нужен талант. Итальянский математик 15 века Лука Пачоли  приводит 8 способов. Познакомимся с некоторыми из них.

Рассмотрите прием внетабличного умножения.

Двадцать умножить на три равно шестидесяти.

Воспользуемся правилом перестановки множителей, получим пример, который умеем решать.

Прочитайте правило внимательно.

При умножении круглого числа на однозначное, надо умножить десятки на второй множитель, в ответ справа добавить нуль.

Увеличить в десять раз — это значит написать в значение произведения первый множитель и добавить к нему 0 справа.

Произведение семи и десяти равно семидесяти.

Воспользуйтесь правилами математики внетабличного умножения и деления для решения примеров:

Проверьте:

Ошибок нет, молодцы. Ваша первая награда — красная ленточка.

Впереди ждут новые открытия, не отставайте, думайте, решайте.

Видеоурок: Умножение чисел, оканчивающихся нулями по предмету Математика за 4 класс

300 – это три сотни.

15 сотен – это 1500.

Запишем ответ:.

210 000 – это 21 десяток тысяч.

84 дес. тыс. – это 840 000.

Запишем ответ:.

Рассмотрим, как выполнять умножение чисел, оканчивающихся нулями, столбиком на примерах.

Запишем множители в столбик. Запишем 6 под десятками, ведь вы знаете, что при умножении любого числа на ноль получится ноль, поэтому умножение можно начинать с десятков, а ноль потом перенести в результат.

Умножаем десятки. Пишем 2 в десятки, а одну сотню запоминаем и потом добавим к сотням.

Умножаем сотни. и еще та сотня, которую запоминали. Пишем 25 сотен.

Перенесем ноль в результат. Читаем ответ «две тысячи пятьсот двадцать».

Ответ:.

Запишем множители в столбик. Как мы уже сказали, при умножении на нули всегда будут получаться нули, поэтому множитель 7 записываем под сотнями и начинаем умножение с сотен.

 Пишем 8 в сотни, а две тысячи запоминаем и потом добавим к тысячам.

Умножаем единицы тысяч., и еще те 2 тысячи, которые запоминали Пишем 37 тыс.

Нули переносим в ответ

Читаем ответ «тридцать семь тысяч восемьсот».

Ответ:.

­

Запишем множитель 3 под тысячами, поскольку при умножении на нули получим нули.

 это мы знаем.

Перенесем нули в ответ:

Читаем ответ «триста шестьдесят девять тысяч».

Ответ:.

Заключение

На этом уроке мы научились умножать многозначные числа, оканчивающиеся нулями, на однозначное число.

Список литературы

1. Петерсон Л.Г. Математика. 4 класс. Учебник в 3 ч. – М.: 2013. – 96 с. + 128 с. +96 с.
2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2010.
3. Демидова Т.Е., Козлова С.А., Тонких А.П. Математика. 4 класс. Учебник в 3 ч. . 2-е изд., испр. – М.: 2013.; Ч.1 – 96 с., Ч.2 – 96 с., Ч.3 – 96 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. Вычисли
2. Сколько нулей будет в ответе?
3. Вычисли:

Диагностика и лабиопластика

Для постановки диагноза врачу достаточно осмотреть женщину на гинекологическом кресле. Ввиду того, что повлиять на величину кожных складок с помощью консервативных методов лечения невозможно, пациентка должна принять решение о необходимости проведения интимной пластики. Лабиопластика, или хирургическая коррекция половых губ, не имеет строгих показаний.

Если женщина решается на ее проведение, ей рекомендуют:

• получить консультацию гинеколога, который во время осмотра возьмет мазок на флору;
• сдать клинический анализ крови и мочи;
• сдать биохимический анализ крови, а также анализы на гепатиты Б и Ц, сифилис, СПИД;
• сделать коагулограмму – это исследование позволяет определить качество свертываемости крови.

Важно! При применении общей анестезии во время операции пациентке советуют дополнительно сделать электрокардиограмму. В зависимости от величины половых губ и ожидаемого результата хирург может выполнять:

В зависимости от величины половых губ и ожидаемого результата хирург может выполнять:

• V-образную, или клиновидную резекцию, при которой с каждой стороны складки вырезаются лоскуты V-образной формы, позволяющие уменьшить их размеры, сохранив при этом привычный вид;
• линейную – в этом случае после хирургического вмешательства кожные складки принимают неестественный прямолинейный вид вследствие нарушения складчатости и формы.

У обоих вариантов есть существенный недостаток, заключающийся в продолжительном реабилитационном периоде. Единственный выход из ситуации – лазерная лабиопластика. Это щадящая методика, при которой используется лазерный луч, минимизирующий развитие кровотечения и появление рубцов и шрамов. Между тем, его не рекомендуют проводить нерожавшим женщинам.

Как объяснить ребенку умножение столбиком?

• Если вы дома решили провести урок по математике, изучить, как производить умножение в столбик, то превратите ваше занятие в игру.
• Постепенно, терпеливо объясняя, как это делается. Отвечайте на все вопросы школьника, чтобы ему было понятно, что и за чем делать.
• Дайте вначале для примеров несложные примеры, а потом уже выбирайте задания потруднее.

Умножение для детей

Что необходимо знать для умножения натуральных чисел столбиком?

Промежуточные вычисления при умножении столбиком проводятся с использованием , поэтому ее желательно знать наизусть, чтобы не тратить время на поиск нужного результата.

Рано или поздно при умножении столбиком мы столкнемся с умножением однозначного натурального числа на нуль. В этом случае мы будем пользоваться : a·0=0, где a – произвольное натуральное число..

Рекомендуем разобраться с материалом статьи сложение столбиком. Это связано с тем, что на одном из этапов умножения в столбик приходится складывать промежуточные результаты (которые называют неполными произведениями), используя принцип сложения столбиком.

Также нам пригодятся навыки сравнения натуральных чисел.

Наконец, желательно вспомнить .

Деление многозначных чисел

Деление столбиком может показаться детям сложным, однако запомнить алгоритм несложно. Рассмотрим деление многозначных чисел на однозначное число:
215 : 5 = ?
Записывается вычисление следующим образом:
Под делителем будем записывать результат. Деление выполняется следующим образом: сравниваем крайнюю левую цифру делимого с делителем: 2 меньше 5, разделить 2 на 5 мы не можем, поэтому берем еще одну цифру: 21 больше 5, при делении получается: 20 : 5 = 4 (остаток 1)

Сносим к полученному остатку следующую цифру: получаем 15. 15 больше 5, делим: 15 : 5 = 3

Решение будет выглядеть таким образом:

Так производится деление без остатка. По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.

Если необходимо произвести деление трехзначных чисел в столбик на двухзначное, порядок действий будет таким же, как при делении на однозначное число.

Приведем примеры на деление:

Аналогично проводится вычисление при делении многозначного числа на двузначное с остатком: 853 : 15 = 50 и ( 3 ) остатокОбратите внимание на эту запись: если при промежуточных вычислениях в результате получается 0, но пример не решен до конца, ноль не записывается, а сразу сносится следующая цифра, и вычисление производится дальше. Поможет усвоить правила деления многозначных чисел в столбик видеоурок

Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными

Поможет усвоить правила деления многозначных чисел в столбик видеоурок. Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными.

Важно! Следите за записью: разряды должны записываться под разрядами, в столбик. Видео «Деление в столбик»

Видео «Деление в столбик»

Если во 2 классе ребенок выучил таблицу умножения, примеры на умножение и деление двузначного или трехзначного числа на уроках математики за 4 класс не вызовет у него трудностей.

Читайте так же:

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Советы тем, кто хочет хорошо знать математику

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Умножение на двузначное число

Умножение на двузначное число

Двух-, трех-, четырехзначные числа можно умножить на однозначные в уме. Когда ребенок станет немного старше, он так и будет делать. Но умножать на двухзначное число в уме ему еще сложно. Поэтому применяется снова действие в столбик.

Пример: Делаем умножение на двузначное число — 45х75:

• Под числом 45 записываем 75 по правилу: единицы под единицами, десятки под десятками
• Умножение начинаем делать с единиц: 25 — 5 пишем, 2 запоминаем, чтобы потом прибавить к десяткам
• Умножаем 5 на 4, получается 20. Прибавляем к десяткам 2, получается 22. Записываем впереди цифры 5, получается 225
• 7х5=35. Цифру 5 записываем под десятками, 3 запоминаем и будем ее записывать потом в сотни
• 7х4=28 сотен. Прибавляем 3, получается 31 сотня. Записываем по правилу умножения в столбик
• Складываем неполные произведения — единицы, десятки и сотни и получаем результат: 45х75=3375

Как умножать десятичные дроби столбиком

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

1

Выполняем умножение столбиком, не обращая внимание на запятые

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63,37 и ,12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3,37·,12=7,6044.

Пример 5

Подсчитайте, сколько будет 3,2601 умножить на ,0254.

Решение 

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3,2601·,0254=,08280654.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 3/5 на 0,9.

Как решаем:

1. Записать 0,9 в виде обыкновенной дроби:

   0,9 = 9/10.

2. Умножить числа по правилам
   3/5 ∗ 9/10 = 27/50 = 0,54.

Ответ: 3/5 ∗ 0,9 = 0,54.

Пример 2. Умножить 0,18 на 3 1/4.

Как решаем:

1. Записать 3 1/4 в виде десятичной дроби:

   3 1/4 = 3,25.

2. Произвести умножение в столбик или при помощи калькулятора:

   0,18 ∗ 3,25 = 0,585.

Ответ: 0,18 ∗ 3 1/4 = 0,585.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Как умножать десятичные дроби в столбик

Чтобы перемножить десятичные дроби нужно сделать три шага:

1. Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.
2. Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.
3. Полученную цифру отсчитать справа налево и поставить запятую.

Пример 1. Перевести 5,4 в смешанное число.

Как решаем: Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых: Получаем: 311 ∗ 001 = 311. Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую). Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы

Ответ: 3,11 ∗ 0,01 = 0,0311.

Примеры умножения десятичных дробей столбиком:

Чтобы закрепить тему, смотрите видео «Умножение десятичных дробей».

Как умножать столбиком? Как объяснить ребенку умножение столбиком? Умножение на однозначное число, двузначное число, трехзначное число: алгоритм умножения чисел

Ребенка просто научить умножать столбиком, если делать это в игровой форме.

Математика — это сложная наука почти для каждого ребенка

Родителям приходится заставлять своего чада выполнять домашние задания, ведь это необходимо не только для получения хороших оценок в школе, но и для развития
Напряженная работа мозга помогает развить память, интеллект, внимание и приобрести отличные навыки счета
Все качества, приобретенные в школе, будут полезными в будущей жизни. Считать нужно уметь не только ученым, но и рабочим, и домохозяйкам

Одно из самых сложных действий — это умножение. Оно дается сразу не каждому ребенку

Как объяснить ребенку умножение столбиком?

Как объяснить ребенку умножение столбиком?

Научить ребенка умножению — это реальная задача, но придется запастись терпением. Занятие должны быть регулярными, ведь только система поможет добиться желаемых результатов.

• Расскажите ребенку, что умножение — это повторение, сложение одинаковых чисел
• Напишите на листе бумаги примеры: 2+2+2+2+2 и 2х5
• Сделайте вместе с ребенком сравнение, как быстрее подсчитать сложением или умножением
• Чтобы закрепить эту полученную информацию, приведите примеры из жизни, но они должны быть не выдуманными. Например, к ребенку в гости идут 7 друзей. Для них готово лакомство — по 2 конфеты. Как быстрее подсчитать — сложением или умножением? Подсчитайте вместе с малышом и запишите на бумаге в виде примера: 7х2=14

Когда пройдет несколько занятий, таблица умножения будет выучена, тогда можно начинать объяснять ребенку умножение столбиком двухзначных и трехзначных чисел.

Умножение на однозначное число

Умножение на однозначное число

Дети уже в третьем классе начинают проходить умножение в столбик на двухзначные и трехзначные числа. Но сначала необходимо объяснить умножение на однозначное число, например, 76х3:

• Сначала умножаем 3 на 6, получается 18 — 1 десяток и восемь единиц, 8 единиц пишем, а 1 запоминаем. Единицу мы потом будем прибавлять к десяткам
• Теперь умножаем 3 на 7, получается 21 десяток + единица, которую запоминали, получилось 22 десятка
• Используем правило умножения в столбик: последнюю цифру оставляем, а ниже записываем десятки, получилось 228

Умножение на двузначное число

Умножение на двузначное число

Двух-, трех-, четырехзначные числа можно умножить на однозначные в уме. Когда ребенок станет немного старше, он так и будет делать. Но умножать на двухзначное число в уме ему еще сложно. Поэтому применяется снова действие в столбик.

Пример: Делаем умножение на двузначное число — 45х75:

• Под числом 45 записываем 75 по правилу: единицы под единицами, десятки под десятками
• Умножение начинаем делать с единиц: 25 — 5 пишем, 2 запоминаем, чтобы потом прибавить к десяткам
• Умножаем 5 на 4, получается 20. Прибавляем к десяткам 2, получается 22. Записываем впереди цифры 5, получается 225
• 7х5=35. Цифру 5 записываем под десятками, 3 запоминаем и будем ее записывать потом в сотни
• 7х4=28 сотен. Прибавляем 3, получается 31 сотня. Записываем по правилу умножения в столбик
• Складываем неполные произведения — единицы, десятки и сотни и получаем результат: 45х75=3375

Умножение на трехзначное число

Умножение на трехзначное число

Есть такие люди, которые производят умножение трехзначных чисел в уме. Ребенку, естественно, сложно это делать, поэтому он должен оттачивать навыки на бумаге.

Умножение на трехзначное число производится по такому же принципу, как и умножение на двухзначное число:

• Сначала умножаются единицы и записываются в строку
• Ниже будут записаны десятки по правилу умножения в столбик
• Третьей строкой записывается произведение сотен
• В итоге получатся тысячи, сотни, десятки и единицы, которые нужно сложить

Как умножать столбиком двузначные числа?

Как умножать столбиком двузначные числа

Как умножать столбиком двузначные числа мы рассмотрели выше, а как умножить большое число на двузначное следует разобрать подробнее:

Пример: 4325х23

• Сначала умножаем 3 на 5, на 2, на 3 и на 4. Записываем единицы, десятки, сотни и тысячи
• Теперь умножаем 2 на 5, на 2, на 3 и на 4. Также записываем, но уже десятки под десятками, сотни под сотнями, а тысячи под тысячами
• Складываем по правилу и получаем результат: 4325х23=99475

Алгоритм умножения чисел

Алгоритм умножения чисел

Алгоритм умножения чисел заключается в применении таблицы умножения. Поэтому ребенок сначала должен досконально выучить таблицу умножения, а потом учиться выполнять действие со сложными числами.

Игры на умножение

Игры на умножение

Игры на умножение:

Ребенку будет легче запомнить таблицу умножения в стихотворной форме, а занимательный персонаж поможет ему в этом.

Развитие памяти тренажёр и теория

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Решим пример \(\textcolor{red} {295383\div 34}\).

Далее записываем известные
компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру
разряда тысяч, а под неполным делимым пишем результат произведения неполного
частного и делителя. И сразу же находим остаток от этого действия, т.е.
вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor{red} {8\cdot 37=272}\). Записываем его под 295 и находим разницу: \(\textcolor{red} {295-272=23}\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

Находим результат деления второго неполного делимого на делитель. 233 сотни разделить на 34 будет 6 сотен. Значит, в разряде сотен частного будет цифра 6. Умножаем ее на делитель 34, получаем 204 и еще 29 сотен неразделенных.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

При делении второго неполного делимого 298 десятков на делитель 34 получается 8 десятков, и еще 26 десятков неразделенных (как и в предыдущих действиях, я умножил 8 на 34 и результат отнял от 298). Поэтому, в частном, в разряде десятков записываем цифру 8.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Разделив 263 единицы на 34, получаем 7 полных единиц и 25 неразделенных. Записав в частном последнюю цифру разряда единиц, получаем окончательный ответ действия \(\textcolor{red} {295383\div 34=8687}\) и 25 в остатке.

Рассмотрим еще один пример. \(\textcolor{red} {25326\div 63}\).

Первое неполное делимое будет 253 сотни, количество цифр в частном – 3.

Делим 253 сотни на 63, получается 4 полных сотни и неразделенная 1 сотня в остатке.

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Но 12 не делится нацело на 63 части, то есть, нет ни одного целого десятка в каждой части. Значит, мы в частном в разряде десятков должны записать , поскольку все 12 десятков оказались неразделенными. А к этим 12 десяткам (т.е. 120 сотням) добавить (снести) 6 единиц делимого.

Итак, запомните, что
каждое неполное делимое образует в частном одну цифру соответствующего разряда
и что даже если неполное делимое меньше делителя, то в частном все равно нужно
записать нулевой результат этого действия.

126 единиц делим на 63, получается 2 единицы без остатка. Теперь мы можем записать окончательный ответ деления \(\textcolor{red} {25326\div 63=402}\).

Итак, в общем виде алгоритм деления в столбик выглядит так:1. Находим первое неполное делимое и количество цифр в частном.2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.4. Ставим между ними знак минус и выполняем действие.5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.7. Если неполное делимое невозможно разделить на делитель, то в частном ставится и к этому неполному делимому сносится следующая цифра.

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8
• 7,42
• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков.

• Однозначное — состоит из одного знака
• Двузначное — из двух
• Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.

Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения 1. От перестановки множителей местами произведение не меняется. a * b = b * a 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c) Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.

Важно помнить правило: умножение в столбик с нулями дает в результате ноль

а * 0 = 0, где а — любое натуральное число.

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения

Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д

3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

5. Складываем то, что нашли и получаем ответ.

Умножение на однозначное число

Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше. 

Возьмем пример 234 * 2:

1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.

2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.

3. Ответ запишем под чертой:

Производить действия необходимо в следующей последовательности:

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость

Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем

Повтори тему — деление в столбик, она очень полезная!

Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов. А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.

Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.