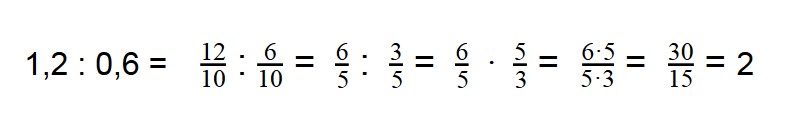Как научить ребенка решать и считать примеры в пределах 20: алгоритм обучения и советы педагогов

Приемы сложения и вычитания вида□ + 6, 7, 8, 9, □–6, 7, 8, 9

Поселились все зверюшки вместе в теремке. И дружно вместе принялись записывать остальные таблицы. Все примерах в них составляются на основе тех правил, о которых напомнила нам лисичка. Давай поможем им.

Начнем с таблицы сложения числа 6.

В предыдущих таблицах есть только четыре примера, в которых встречается слагаемое 6. Найди их.

Вот что выписали зверята.

Теперь переставляем слагаемые местами.

А теперь из этой таблицы мы легко можем составить таблицу вычитания числа 6. Попробуй сделать это самостоятельно.

Посмотри, какую таблицу вычитания числа 6 записали наши друзья.

Вот мы и закончили! У нас получилось составить таблицы сложения и вычитания числа 6.

Продолжаем. С таблицей сложения числа 7 нам повезло еще больше, ведь в ней будет всего три примера. Ты уже нашел их? Вот что записали зверята.

Надеюсь, ты не забыл еще переместительное свойство действия сложения, ведь оно нам пригодится при составлении таблицы с числом 7.

Подумай над этим сам. А потом проверь.

Все правильно. Теперь из предыдущей таблицы составим таблицу вычитания числа 7.

Не спеши, сделай это самостоятельно.

Проверь свою таблицу.

Как быстро ты со всем справился.

Дальше будет еще легче. Вспомни примеры, где встречается слагаемое 8.

В таблице сложения числа 8 всего два примера. Составь их.

Давай проверим.

Теперь составь таблицу вычитания числа 8.

Вот что получилось у наших друзей.

Вот мы и выучили таблицы сложения и вычитания с числом 8.

Ты, наверное, уже немного устал. Но нам осталось познакомиться всего с одной таблицей. Это таблица сложения и вычитания с числом 9.

Ты уже нашел пример с числом 9? Уверена, что ты справился. Назови его.

9 + 1 = 10

Давай переставлять. Что у нас получится?

1 + 9 = 10

Вот и вся таблица сложения с числом 9. Переходим к таблице вычитания числа 9.

У тебя уже все готово?

Правильно.

10 − 9 = 1

Мы с тобой неплохо потрудились и составили все таблицы в пределах 10. Вот как выглядит общая таблица сложения.

В этой таблице красным цветом выделены примеры, которые составлены путем перестановки слагаемых. Их запомнить очень легко.

А вот общая таблица вычитания чисел в пределах 10.

В этой общей таблице хорошо видны несколько закономерностей, которые помогут тебе лучше и быстрее запомнить результаты указанных математических выражений на вычитание.

1. В результате вычитания числа 1 получается число, которое является предыдущим по отношению к уменьшаемому.
2. В примерах, где уменьшаемое и вычитаемое являются «соседями» в натуральном ряду чисел, разность равна 1.
3. В таблице есть «парные» примеры, которые можно составить из одного и того же примера на сложение.

В этих выражениях компонентами являются одни и те же числа. Присмотрись и найди другие подобные пары примеров.

Чтобы получше запомнить все примеры из таблиц сложения и вычитания чисел в пределах 10, почаще тренируйся. Не забудь о наших сегодняшних помощниках.

Таблицы сложения и вычитания числа 1 мы выучили с помощью мышки, которая переходила маленькими шагами с числа на соседнее число. Как найти результаты в таблицах сложения и вычитания числа 2 нам подсказала лягушка, которая умеет прыгать через число. Зайчик показал, как узнать ответы в примерах из таблиц сложения и вычитания числа 3, который скачет так высоко, что может перепрыгнуть через два числа сразу. А двойной прыжок лягушки поможет вспомнить результаты таблиц сложения и вычитания числа 4. Лисичка же разгадала закономерности составления всех остальных таблиц.

Обязательно используй все приемы, которые нам подсказали герои нашей сказки. Чем чаще ты будешь повторять примеры из таблиц, тем быстрее ты запомнишь результаты каждого из них. Надеюсь, ты легко справишься с проверочными заданиями к этому уроку.

Поурочные разработки по Математике 1 класс — «Школа России» Ситникова Т. Н. — 2016

Таблица сложения — ЧИСЛА ОТ 1 ДО 20. СЛОЖЕНИЕ И ВЫЧИТАНИЕ

Цели: составить таблицу сложения в пределах 20 и провести работу, направленную на ее запоминание; развивать умение решать составные задачи.

Планируемые результаты: учащиеся научатся выполнять сложение чисел с переходом через десяток в пределах 20; использовать математическую терминологию при составлении и чтении математических равенств; решать составные задачи с недостающими данными в условии; выполнять задания творческого и поискового характера; контролировать и оценивать свою работу и ее результат.

Ход урока

I. Организационный момент

II. Актуализация знаний

1. Устный счет

(Учащиеся по очереди выходят к доске, решают примеры и вписывают ответы в окошки.)

2. Логическая разминка

— Решите задачи.

• Батон и пачка сахара весят больше, чем батон и конфеты. Что весит больше: сахар или конфеты? (Сахар.)

• Г руша тяжелее, чем яблоко, а яблоко тяжелее персика. Что тяжелее: груша или персик? (Груша.)

• За пакет муки, пачку сахара и пачку кофе уплатили дороже, чем за такой же пакет муки, пачку сахара и булку. Что дороже: кофе или булка? (Кофе.)

3. Работа над задачами

— Составьте задачи по рисункам и выражениям.

5 — 3

5 + 3

5 — 3

3 + 2

5 — 2

— Почему выражение 5 — 3 записано два раза?

III. Самоопределение к деятельности

— Рассмотрите выражения в каждом столбике.

8 + 3	6 + 6	7 + 6	7 + 7
7 + 4	7 + 5	8 + 5	8 + 6
6 + 5	8 + 4	9 + 4	9 + 5
…	…	…	…

— Как изменяется первое слагаемое? второе слагаемое?

— Изменится ли сумма?

— Что общего в примерах каждого столбика? (Одинаковые ответы.)

— Придумайте пример в каждый столбик так, чтобы надо было прибавлять по частям.

— Откройте учебник на с. 72. Прочитайте тему урока.

— Мы знаем уже все случаи сложения, когда надо прибавлять по частям. Почему в красной рамке записаны эти же примеры?

— Поставьте задачи урока.

IV. Работа по теме урока

Работа по учебнику

— Сравните примеры каждого столбика.

— Что изменяется в примерах каждого столбика? (Второе слагаемое. )

— Как оно изменяется? (Увеличивается на 1.)

— Как это влияет на сумму? (Если первое слагаемое не изменяется, а второе слагаемое увеличивается на 1, то и сумма увеличивается на 1.)

— Сравните примеры в каждой строке.

— Как изменяется первое слагаемое? второе слагаемое?

— Изменяется ли сумма? (Если первое слагаемое уменьшается, а второе увеличивается на одно и то же число, то сумма не изменяется.)

— Прочитайте равенства в третьем столбике разными способами.

— Закройте ответы во втором столбике, оставив первый пример открытым. Как узнать ответы в остальных примерах?

— 13 — это 7 и сколько?

— К какому числу прибавили 6, если получили 11?

— На сколько увеличили 9, если получили 18?

— Какое число надо увеличить на 9, чтобы получить 13?

— Сумма каких двух чисел равна 14?

(Учитель задает еще несколько подобных вопросов.)

№ 1 (с. 72).

(Первое задание учащиеся выполняется устно с комментированием, второе задание — под руководством учителя с целью подготовки к изучению табличного вычитания. Далее работа в парах по карточкам. Каждый ученик достает из конверта по пять карточек с примерами. Учащиеся по очереди показывают пример соседу, тот называет ответ, затем карточка переворачивается и ответ проверяется.)

V. Физкультминутка

Раз, два — наклонилися слегка.

Три, четыре — руки в боки, будем делать многоскоки.

Пять, шесть — на лесенку надо залезть.

Семь, восемь — пробежаться вас попросим.

Девять, десять — вот и все.

Скоро встретимся еще.

VI. Закрепление изученного материала

1. Работа по учебнику

№ 2 (с. 72),

— Как узнать, на сколько одно число больше или меньше другого?

— Известен ли рост Даши и Наташи?

— Что известно в задаче?

— Если девочки были весной одинакового роста, то какие числа мы будем сравнивать?

— Что значит “выше”?

— Запишите решение задачи самостоятельно.

№ 3 (с. 72).

(В первой задаче учащиеся подбирают данные самостоятельно

При подборе данных во второй задаче учителю необходимо обратить внимание детей на то, что сумма чисел — цен ручки и блокнота — должна быть меньше 10 руб. Решения и ответы учащиеся записывают самостоятельно

Проверка.)

2. Работа в тетради с печатной основой

№ 1-3 (с. 38).

VII. Рефлексия

(Выполнение заданий в тетради для проверочных работ (с. 44—45). Дополнительно можно предложить задание на полях. Взаимопроверка.)

— Оцените своего соседа по парте:

• молодец, все решено правильно;

• хорошо, ошибки есть, но совсем немного;

• тебе нужна помощь учителя.

— Какие задачи мы ставили в начале урока?

— Кто смог назвать без ошибок все примеры, когда вы выполняли задание в парах?

VIII. Подведение итогов урока

— Как таблица поможет нам считать быстро?

— Как поступить, если не помнишь ответ в одном из примеров в столбике?

ПредыдущаяСледующая

Вычитание единиц из произвольных чисел

Будем считать, что уменьшаемое можно представить в виде суммы разрядных слагаемых. Подобные случаи мы рассматривали в предыдущих параграфах.

Определение 3

Чтобы вычесть из такого числа однозначное число, нужно уменьшаемое разложить по разрядам, после чего вычесть число из суммы.

Рассмотрим типичные примеры, которые помогут усвоить материал.

Пример 16

Необходимо определить разность чисел 46 и 2.

Число 46 представляем как 40+6, тогда 46−2=(40+6)−2=40+(6−2)=40+4=44. Для того, чтобы усложнить задание, найдем разность 46 и 8. Имеем 46−8=(40+6) −8. Так как 8 больше, чем 6, то: (40+6) −8=(40−8) +6. 40−8 вычислим по примеру: 40−8=(30+10) −8=30+(10−8) =30+2=32. Тогда (40−8) +6=32+6=38. Теперь отнимем от 6 047 число 5. Раскладываем 6 047 и вычитаем число из суммы: 6 047−5= (6 000+40+7) −5=6 000+40+(7−5) =6 000+40+2=6 042

Закрепим навыки еще одним примером.

Пример 17

Необходимо вычесть из числа 2 503 число 8.

Раскладываем и получаем: 2 503−8= (2 000+500+3) −8. Так как 8 больше, чем 3, но меньше, чем 500, то (2 000+500+3) −8=2 000+(500−8) +3. Вычислим разность 500−8, для этого представляем число 500 в виде суммы 400+100=400+90+10 (при необходимости вернитесь к предыдущему пункту этой статьи) и выполняем необходимые вычисления:500−8=(400+90+10) −8=400+90+(10−8) =400+90+2=492. 2 000+(500−8) +3=2 000+492+3=2 495.

Вычитание натурального числа из суммы чисел

Чтобы найти разность суммы двух чисел и числа, необходимо сначала вычислить сумму, из которого вычитается число. Чтобы упростить процесс вычитания, можно воспользоваться определенным свойством вычитания. Рассмотрим несколько примеров.

Пример 4

Необходимо вычесть из суммы 50+8 натуральное число 20.

Сумма 50+8 – это сумма разрядных слагаемых числа 58. Ищем варианты решения. Используем приведенное выше правило вычитания: так как 20<50, то справедливо равенство (50+8) −20=(50−20) +8. Можем сделать вывод, что 50−20=30 (5 десятков – 2 десятка), тогда (50−20) +8=30+8. Искомое число – 38.

Решение можно представить в виде цепочки равенств: (50+8)−20=(50−20)+8=30+8=38.

Пример 5

Необходимо вычесть из суммы  21+8 число 3. Так, как и 3<21 и 3<8, то справедливы равенства (21+8) −3=(21−3) +8 и (21+8) −3=21+(8−3).

Выберем наиболее подходящий вариант вычисления. Вычитаем из меньшего числа. В примере 8<21. Итак, (21+8) −3=21+(8−3) =21+5=26.

Усложним пример. Необходимо вычислить разность числа 20 из суммы 20 000+6 000+300+50+1. Воспользуемся свойством вычитания, которое мы изучили выше.

Вычислить разность довольно легко: (20 000+6 000+300+50+1) −20=20 000+6 000+300+(50−20) +1==20 000+6 000+300+30+1=26 331.

Рассмотрим решение еще одного примера: (107+42+9)−3=107+42+(9−3)=107+42+6=155.

Вычитание суммы чисел из натурального числа

Определение 2

Чтобы вычесть сумму двух чисел из натурального числа, необходимо вычислить сумму, после чего провести вычитание.

Можно использовать свойство вычитания, приведенное выше. Рассмотрим несколько примеров.

Пример 6

Необходимо вычесть из числа 100 сумму 90+8.

Согласно свойству, получаем: 100−(90+8) =(100−90) −8. Находим 100−90=10.

Представим вычисление как: (100−90) −8=10−8=2.

Пример 7

Необходимо найти разность числа 17 и суммы чисел 8 и 4.

Получаем, что: 17−(8+4) =(17−8) −4. Воспользуемся таблицей и получаем, что 17−8=9, тогда (17−8) −4=9−4=5. Можно кратко записать решение как: 17−(8+4) =(17−8) −4=9−4=5.

Правая часть равенства a−(b+c) =(a−b)-c иногда записывается в виде a−(b+c)=a−b−c. В этом случае подразумевается, что a−b−c=(a−b) −c. Разность 15−(7+2) можно представить, как 15−7−2. Вычисляем разность – отнимаем от 15 число7. Вычитаем 2из полученного результата.

Таким образом, 15−(7+2) =15−7−2=8−2=6.

Используя свойство вычитания и сочетательное свойство сложения, можно найти разность суммы двух, трех и более чисел.

Пример 8

Необходимо выполнить вычитание из числа 1 000 суммы трех чисел вида 900+90+1.

Сумму 900+90+1 представим, как 900 и 90+1, то есть, 900+90+1=900+(90+1) (изучите подходящий раздел для лучшего понимания). Используем свойство вычитания, изученное выше: 1 000−(900+(90+1)) = (1 000−900) −(90+1). Так как 1 000−900=100, то (1 000−900) −(90+1) =100−(90+1). Вычитаем сумму из числа: 100−(90+1) =(100−90) −1=10−1=9.

Краткая запись решения имеет вид: 1 000−(900+90+1) = (1 000−900) −(90+1) =100−(90+1) =(100−90) −1=10−1=9

Разность 1 000−(900+90+1) также может выглядеть как ((1 000−900) −90) −1. Можно записать это по-другому как 1 000−900−90−1. В этих случаях сначала находится разность первых двух чисел, далее от полученного результата вычитается третье число и так далее.

Пример 9

Необходимо вычесть из числа 20 сумму чисел 10, 4, 3 и 1. Получаем, что: 20−(10+4+3+1) =20−10−4−3−1=10−4−3−1=6−3−1=3−1=2.

Таблица сложения до 20

Сложим 3 и 4. Находим число 3 по горизонтали и число 4 по вертикали. Мысленно проводим линии до места пересечения. Это и есть искомое значение. Нетрудно заметить, что если мы поменяем местами значения и отыщем по горизонтали 4, а по вертикали – 3, то также в ячейке будет 7.

Отсюда вытекает одно из свойств, справедливых для суммы чисел. Звучит оно так: «От перестановки мест слагаемых сумма не меняется». Это свойство справедливо и для большего количества слагаемых. Разберемся в вопросе о том, можно ли данной таблицей пользоваться в случае сложения нескольких слагаемых. Ответ: можно, но до определенных значений. В этом случае действия нужно производить постепенно. Сначала складываем первые два слагаемых, получаем некое число. Если это простое число, которое входит в таблицу, то мы находим его и к нему прибавляем оставшееся и так далее. То есть, ориентируемся на наличие значений в таблице. Например, 4+5+6. Начала находим результат для действия 4 + 5, в ячейке на пересечении их столбца и строки находится 9. Далее выполняем действие 9+6. Находим в таблице 9 и 6. Далее все аналогично. Для больших чисел обычно таблицы не составляются. Таблица вычитания. Этой же таблицей можно пользоваться и для операции вычитания. В этом случае производим обратные действия. В самой таблице находим значение, из которого нужно вычесть число. Затем проводим линию до того числа, которое вычитается, остается мысленно дойти до оставшегося значения. Оно и будет искомым. Совсем просто это можно осуществить при помощи линейки. В данном случае линейка подставляется от вычитаемого числа сначала вертикально, затем горизонтально. Или наоборот. Для быстрого устного счета часто запоминают результаты сложения, и со временем уже нет необходимости наличия таблицы перед глазами.

Для ознакомления также ниже представлены более старые варинты таблицы.
 

Таблицы сложения значительно упрощают повседневный счет, поэтому много лет назад люди начали их использовать и некоторые из них мы можем видеть в сохранившихся книгах. Например, так выглядела таблица сложения в книге «Арифметика» Магницкого Л. Ф. 1703 года издания.

(на картинке фото фрагмента из оцифрованной версии книги, саму книгу найти было достаточно сложно, поэтому использована сканированная версия, которая есть в широком доступе) Так выглядит эта таблица в воспроизведении (переиздании) той же книги, сделанном в 1914 году под редакцией П. Баранова:
(на картинке как раз фотография тоже сканированной версии переиздания 1914 года).

Вычитание чисел на координатном луче

Рассмотрим, что такое вычитание геометрической точки зрения. Используем координатный луч. Вычитание из a числа b на координатном луче находится так: определяем точку, координатой является a. Откладываем в направлении точки O единичные отрезки в количестве, определяемом вычитаемым b. Так мы найдем точку на координатном луче, координата равна разности a−b. Другими словами, это перемещение влево из точки с координатой a на расстояние b, попадая в точку с координатой a−b.

Рассмотрим вычитание на координатном луче с помощью рисунка. Так мы попадем в точку с координатой 2 так, что 6−4=2.

Эта сложная наука – математика

Некоторым деткам научиться математическому счету бывает намного труднее, чем, например, научиться читать. Поэтому, чтобы у ребенка появилась так называемая «симпатия» к предмету, родителям придется постараться привить любовь ребенка к математике.

Некоторые родители не желают обременять себя подобными делами и перекладывают обучение вычислениям на плечи педагогов начальной школы. Безусловно, именно учителя и выполняют обучение счету детей, но родители не должны самоустраняться, а обязаны помогать ребенку, помогать находить ошибки, анализировать их.

Даже если вы решили воспользоваться услугами репетитора, заниматься с ребенком дома все равно придется, ведь учитель задает домашние задания, которые следует добросовестно выполнять. В противном случае знания, не подкрепленные практикой, очень быстро забудутся.

Вычитание из произвольных натуральных чисел

Чтобы вычесть десятки, сотни из числа, нужно уменьшаемое представить как сумму и выполнить вычитание. Разберем данный процесс на нескольких примерах.

Пример 18

Найдем разность 400 и 70.

Разложим 400 как 300+100. Тогда 400−70=(300+100) −70. Согласно свойству, получим: (300+100) −70=300+(100−70) =300+30=330. Также можем отнять от числа 1 000 число 40. Представим, что 1 000−40=(900+100) −40=900+(100−40) =900+60=960.

Согласно правилу, (7 000+900+100) −10=7 000+900+(100−10) =7 000+900+90=7 990.

Пользуемся этим правилом в аналогичных случаях.

Пример 19

Найдем 400 000−70.

400 000 разложим как 300 000+90 000+9 000+900+100, тогда400 000−70=(300 000+90 000+9 000+900+100)−70=300 000+90 000+9 000++900+(100−70)=300 000+90 000+9 000+900+30=399 993

Воспользуемся схожим принципов для вычисления сотен, тысяч и других.

Пример 20

Найдем 5 000−800.

Представим 5 000 как 4 000+1 000. Тогда 5 000−800= (4 000+1 000) −800. Используем свойство: (4 000+1 000) −800=4 000+ (1 000−800). Так как тысяча – это десять сотен, то 1 000−800=200. Таким образом, 4 000+ (1 000−800) =4 000+200=4 200.

Данное правило можно использовать для вычисления. Запомнить его, оно еще не раз вам пригодится.

Пример 21

Найдем разность 140 и 40.

Так как 140=100+40, то 140−40=(100+40) −40. Получаем: (100+40) −40=100+(40−40) =100+=100(40−40)= в силу свойств, а 100+=100.

Найдем 140 – 60. Имеем 140−60=(100+40) −60. Так как 60 больше, чем 40, то: (100+40) −60=(100−60) +40=40+40=80.

Проверка результата вычитания сложением

Проверка результата вычитания двух натуральных чисел базируется на связи между вычитанием и сложением. Там мы выяснили, что если c+b=a, то a−b=c и a−c=b. Если a−b=c, то c+b=a; если a−c=b, то b+c=a. Докажем справедливость данных равенств.

Пусть из a отложили в сторону b, после чего осталось c. Этому действию соответствует равенство a−b=c. Мы вернем отложенные b на место, то плучим a. Тогда можно говорить о справедливости равенства c+b=a.

Теперь мы можем сформулировать правило, позволяющее проверить результат вычитания сложением: нужно к полученной разности прибавить вычитаемое, при этом должно получиться число, равное уменьшаемому. Если полученное число не равно уменьшаемому, то при вычитании допущена ошибка.

Осталось лишь разобрать решения нескольких примеров, в которых выполняется проверка результата вычитания при помощи сложения.

Пример 24

Из 50 было вычтено 42 и было получено 6. Правильно ли было выполнено вычитание?

Проверим полученный результат вычитания. Для этого прибавим к полученной разности вычитаемое: 6+42=48 (если нужно, изучите другие параграфы по данной теме). Так как мы получили число, не равное уменьшаемому 50, то можно утверждать, что вычитание было проведено неправильно. Была допущена ошибка.

Пример 25

Необходимо определить разность 1 024−11 и проверить результат.

Вычисляем разность: 1 024−11=1 024−(1+10)=(1 024−1)−10=1 023−10=1 013.

Теперь выполняем проверку:

1 013+11=(1 000+10+3)+(10+1)==1 000+10+10+3+1=1 000+20+4=1 024

Получили число, равное уменьшаемому, следовательно, разность вычислена правильно. 1 024−11=1 023.

Вычитание вида 17 — □, 18 — □

На центральных полках у нас стоят наборы конструкторов. Посчитал? Здесь 17 наборов.

Сегодня мы продали их больше всего. Целых 9 наборов.

У нас получится такой пример.

Уверена, что у тебя все получилось. Значит ты хорошо усвоил основной прием табличного вычитания с переходом через десяток – вычитание частями. Со временем ты запомнишь все рассмотренные примеры из наших таблицы.

Я собрала их все в общую таблицу вычитания.

Хорошенько заучи примеры. Скоро ты будешь учиться находить значение математических выражений с большими числами. Без знания нашей таблицы ты не сможешь справиться с ними.

Тренируйся, пока у тебя не получится с первого разу выполнить все тестовые задания правильно.

Как производить вычитание разрядов чисел

С помощью таблицы сложения, которую мы рассмотрели выше, можно вычитать десятки из десятков, сотни из сотен, тысячи из тысяч. Так, как мы легко можем работать с простыми числами, так, и по аналогии, можно вычитать десятки и сотни. Например, 6 сотен минус 2 сотни равно 4 сотням, то есть, 600−200=400. Также мы можем использовать таблицу и в других случаях.

Если вспомнить, что одна сотня – это 10 десятков, одна тысяча – это 10 сотен, то мы можем вычислять разность, десятков, сотен, тысяч и других чисел.

Рассмотрим пример.

Пример 2

Необходимо вычислить разность 100−70.

Преобразуем числа как десятки. Получаем десять десятков и семь десятков. Из таблицы сложения получаем 10−7=3, тогда разность 10 десятков и 7 десятков равна 3 десяткам, то есть, 100−70=30.

Пример 3

Необходимо вычислить разность 100 000−80 000.

Так как 100 000 – это 10 десятков тысяч, а 80 000 – это 8 десятков тысяч, а 10−8=2. Получаем, что 100 000−80 000=20 000.

Таблицы сложения и вычитания чисел. Математика 2 класс Богданович. ГДЗ, решебник.

Категория: —>> Математика 2 класс Богданович  
Задание:  —>>   
 81 — 100  101 – 120 



Задание 81.

Прочитай таблицы сложения и вычитания числа 2. Расскажи их наизусть. По записям объясни приёмы сложения и вычитания чисел с переходом через десяток.

Число 2 разложим на разрядные слагаемые 1 и 1, потом от 11 отнимаем 1, будет 10, у нас в уме осталось ещё 1. 10 минус 1, будет 9.

Реши примеры.

11 — 2 — 4 = 5	14 — 1 — 1 = 12	14 — 10 + 6 = 10	10 + 7 + 1 = 18
9 + 2 — 1 = 10	10 — 3 — 7 = 0	15 — 5 — 5 = 5	10 + 3 — 1 = 12

Запиши сумму и разность чисел 9 и 2.

• 9 + 2 = 11 (сумма)
• 9 — 2 = 7 (разность)

Начерти отрезок, который на 2 см длиннее данного.



Мальчик положил в пенал 4 ручки. Их стало 10. Сколько ручек было в коробке сначала?

• 1) 10 — 4 = 6
• Ответ: 6.

Задание 86.

Кто тяжелее? Кто легче? На сколько килограммов?

• Белый гусь тяжелее на 2 кг, чем утка.
• Утка легче на 2 кг, чем гусь.

Задание 87.

Составь задачи по таким данным. Решения задач запиши.

1) Было — 11 Улетело — 2 Осталось — ?

2) Было — 9 Подарили — 2 Стало — ?

• 1) На аэродроме было 11 самолетов. Из них 2 улетело. Сколько самолетов осталось на аэродроме?
  • Решение:
  • 1) 11 — 2 = 9
  • Ответ: 9.
• 2) У Саши было 9 солдатиков и ему подарили еще 2. Сколько стало солдатиков у Саши?
  • Решение:
  • 1) 9 + 2 = 11
  • Ответ: 11

В школу привезли 9 компьютеров, а потом — ещё 2. Сколько всего компьютеров привезли?

• 1) 9 + 2 = 11
• Ответ: 11.

Задание 89.

Прочитай таблицы сложения и вычитания числа 3. Расскажи их наизусть. По записям объясни сложение и вычитание с переходом через десяток.

• Сложение: Число 3 разложим на разрядные слагаемые 1 и 2, потом 9 + 1 = 10, у нас в уме ещё 2, 10 + 2 = 12.
• Вычитание: Число 3 разложим на разрядные слагаемые 2 и 1, потом 12 — 2 = 10, у нас в уме ещё 1, 10 — 1 = 9.

Реши примеры.

12 — 3 + 1 = 10	10 — 1 + 2 = 11	11 — 3 — 5 = 8	4 + 5 + 3 = 12
11 — 2 — 7 = 2	10 + 5 + 1 = 16	18 + 1 + 1 = 20	11 — 2 + 3 = 12

У мальчика 9 копеек, а у девочки на 3 копейки больше. Сколько денег у девочки?

• 9 + 3 = 12
• Ответ: 12.

Задание 92.

У Коли две монеты по 5 копеек и одна монета достоинством 2 копейки. Сколько денег у Коли?

• 1) 5 + 2 = 7
• Ответ: 7 копеек.

Задание 94.

1) Из скольких отрезков состоит ломаная?2) Измерь длину наибольшего отрезка.

• 1) Ломаная состоит из 4-х частей.
• 2) Длина наибольшего отрезка – 5 см 5 мм.

Задание 95.

Составь задачи. Решения запиши.

• В канистре 12 л молока, а в бидончике 3 л. На сколько меньше молока в бидончике?
  • Решение:
  • 1) 12 — 3 = 9
  • Ответ: на 9 л меньше.
• В корзине было 11 кабачков, 2 выпало. Сколько осталось кабачков в корзине ?
  • 1) 11 — 2 = 9
  • Ответ: 9 кабачков осталось.

Задание 96.

Составь примеры. Запиши и реши их.

Числа	Найти	Числа	Найти
10 и 2	Сумму	11 и 2	Разность
11 и 3	Разность	9 и 2	Сумму
12 и 3	Разность	20 и 1	Разность

10 + 2 = 12	11 — 2 = 9
11 — 3 = 8	9 + 2 = 11
12 — 3 = 9	20 — 1 = 19

Задание 97.

Прочитай таблицы сложения и вычитания числа 4. Расскажи их наизусть. По записям объясни сложение и вычитание чисел с переходом через десяток.

Реши примеры.

13 — 3 = 10	7 + 4 = 11	4 + 4 + 4 = 16	14 — 1 — 4 = 9
11 — 4 = 7	6 + 4 = 10	7 + 4 — 3 = 8	11 — 4 + 3 = 10

Задание 99.

На клумбе росло 12 цветков. Для букета срезали … цветков. Сколько цветков осталось?

На клумбе росло 12 цветков. Для букета срезали 7 цветков. Сколько цветков осталось?

• Решение:
• 1) 12 — 7 = 5
• Ответ: 7.

Из каждого примера составь по одному примеру на вычитание.

9 + 2 = 11

7 + 4 = 11

8 + 3 = 11

Таблица сложения и вычитания | Учимся дома

Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать и  распечатать.

Таблица сложения до 20 распечатать и скачать

Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.

Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word.

Таблица сложения.rtf

Таблица сложения.pdf

Таблица вычитания до 20 распечатать и скачать

В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.

Таблица вычитания без ответов распечатать и скачать

Для проверки знания детей и их умения вычитать, можно использовать таблицу вычитания, в которой приведены возможные комбинации примеров. Таблицу вычитания без ответов можно распечатать и дать ребенку для заполнения правильными ответами.

Таблица вычитания без ответов.rtf

Таблица вычитания без ответов.pdf

На основе материалов   print.paint-net.ru