Распечатать

5+ игр для быстрого запоминания таблицы умножения

Чтобы быстро выучить таблицу умножения, ребенку в возрасте 8-10 лет — а именно столько ему во 2-4 классе, когда в программе появляется умножение — стоит подобрать игру по вкусу. Так процесс пойдет намного эффективнее, чем в случае простой зубрежки.

Вот перечень наиболее распространенных и интересных вариантов игрового обучения:

Карточки

Их можно распечатать самостоятельно, а можно приобрести практически в любом детском магазине — настолько эта игра известна и популярна. Набор включает все комбинации множителей из таблицы умножения с ответами на оборотной стороне.

Чтобы быстро выучить их, играть предлагается следующим образом:

1. Игрок тянет пример
2. В случае правильного ответа карточка отправляется в «отбой»
3. В случае неправильного — возвращается в колоду

Повторять перечисленные шаги следует до тех пор, пока в основной колоде не останется карт. За счет того, что сложные примеры возвращаются в стопку и встречаются снова и снова, они запоминаются лучше и прочнее.

Чтобы выучить всю таблицу умножения максимально быстро, попробуйте устроить игру на время. Ребята, занимающиеся во 2-3 классе, наверняка будут в восторге от такой викторины.

Вам на помощь придут развивающие компьютерные игры

Стихотворные примеры

Разучите с ребенком самые простые рифмующиеся примеры из таблицы умножения: пятью пять, шестью шесть и т.д. А можно сразу взять на вооружение стихотворный разбор всей таблицы — например, книгу Андрея Усачева «Таблица умножения в стихах».

Яркие иллюстрации и интересные короткие стишки превратят зубрежку в увлекательную игру. Чтобы быстро выучить таблицу во 2 или 3 классе, такой способ подойдет как нельзя лучше.

Счет на пальцах

Любознательным детям втянуться в обучение наверняка поможет один наглядный прием-хитрость умножения на девять.

Рассмотрим его на примере пятью девять:

1. Смотрим на собственные ладошки
2. Отсчитываем пятый пальчик слева (как показатель множителя 5)
3. Считаем количество пальцев слева от «множителя» — это десятки (в данном примере их будет четыре)
4. Считаем количество пальчиков справа от пятого — это единицы (в данном примере их пять)

Итогом будет число 45 — ответ на пример из таблицы умножения. Такой подход работает для любых умножений на девять — попробуйте сами.

Ни в коем случае не критикуйте ребенка за неудачи

Использование игрушек или наглядных примеров

Чтобы быстро выучить принципы умножения на 2 и 3 по таблице умножения, можно использовать в качестве подспорья в игре практически что угодно: игрушки, предметы на улице, людей, животных и т.д.

Выберите такой пример, который более знаком и привычен вашему ребенку. Выстраивайте в ряд по два и три игрушки и считайте их. Потом объясните ребенку принцип сокращения процесса подсчета с помощью умножения.

Мобильные или онлайн-игры на изучение таблицы умножения

В сети существует бесчисленное количество разных игр, направленных на то, чтобы быстро выучить таблицу умножения, играя онлайн. Подберите вместе с ребенком увлекательную и яркую игру и предоставьте ему развлекаться — а после проверьте успехи.

Если вас заботит неконтролируемое пребывание ребенка в интернете, выберите игру, которую можно бесплатно скачать, и используйте ее, чтобы быстро выучить таблицу умножения.

Есть много способов привлечь внимание ребенка

Морской бой

Этот игровой способ отлично подходит для закрепления уже имеющихся знаний. Запишите поля «морского боя» цифрами с обеих сторон и установите, что для атаки сектора нужно назвать результат умножения соответствующих чисел.

Такая несложная и увлекательная игра отлично тренирует память и скорость умножения. Конечно, чтобы быстро выучить таблицу умножения во 2 классе, игра нужна не всегда.

Некоторые детки, особенно если им повезло со школьными преподавателями и вообще отношением к учебе, с интересом будут постигать принципы математических примеров и без игр.

В этом случае используйте системный пошаговый подход к обучению:

1. Объясните принцип умножения на единицу и десятку
2. Освойте удвоение
3. Разберите принцип неизменности результата от перестановки множителей
4. Выучите квадраты чисел
5. Последовательно переходите к изучению умножения на 3, 4, 5 и т.д.

Настройтесь на позитивный лад, и результат не заставит себя долго ждать

Даже в такой подход можно добавить игровой элемент, помечая разными цветами уже заученные области. Финальной целью игры будет очищение поля.

Запоминание таблицы умножения — одна из первых ступеней в обучении ребенка математике, одна из важнейших основ. 

Мы уверены, что вы выберете оптимальный подход и успешно изучите все тонкости умножения чисел. Больше наглядного материала по игровому изучению таблицы вы сможете найти в этом видео:

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

С чего начать изучение таблицы умножения?

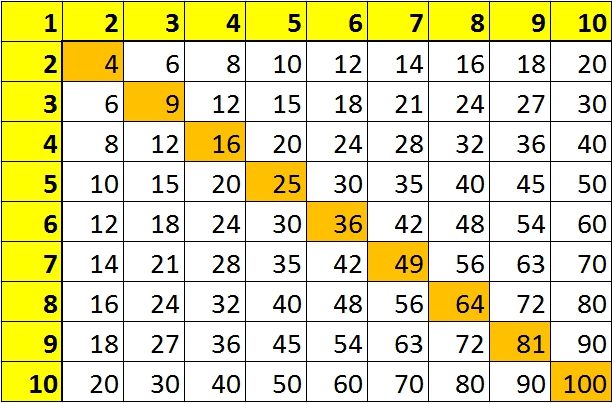
Первый этап подготовки выполните сами – распечатайте таблицу Пифагора и таблицу с примерами

И вот тут важно обратить внимание, что это не одно то же. Во втором случае это просто примеры с готовыми ответами, представленные в столбиках для каждой цифры. Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10

Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10.

Прежде чем выучить наизусть всю таблицу умножения ребенку, покажите ему, что цифры, которые перемножаются, находятся слева и сверху, а если пальчиками от них провести навстречу друг другу, то на пересечении будет результат их перемножения.

Задаваясь вопросом, как быстро выучить таблицу умножения ребенку, и с чего начать этот процесс, то знакомить его с самими действиями нужно, начиная с тех манипуляций с умножением, которые ему понять и выполнить самостоятельно будет проще всего:

• На «1». Любое действие в этом случае дает результат, при котором число остается прежним. Так школьнику будет проще понимать, что это за процесс. Предложите ему попрактиковаться с умножением на один несколько раз с разными числами;
• На «10». Объясните ребенку, что, несмотря на то что это большое число, умножать на него очень просто. Нужно лишь к умножаемому приписывать ноль. Начните с небольших значений – например, 3х10, а потом предложите ему самостоятельно попробовать выполнить действия с большими числами.

На пути к тому, как научить быстро выучить таблицу умножения ребенка, это важные шаги. Теперь он знает, как работать с крайними значениями сетки Пифагора. Помимо практического значения, для него это играет и психологическую роль:

• У школьника сложится понятие того, как нужно работать с ней;
• Он поймет, что начало положено, и ему знакомиться с сеткой не сложно, даже интересно, поэтому полностью ее освоить он сможет.

Если ученик еще не устал, можно приступать к следующему этапу того, как можно быстро выучить таблицу умножения:

Предложите школьнику умножать на «2». Уже с первых классов обучения математике дети знают, как выполнять сложение до 10, в том числе одинаковых чисел. Поэтому занятие будет для обучаемого простым и даже интересным;
Перемена мест множителей

Это важное правило, часто непонятное детям, заключающееся в том, что при перестановке множителей их произведение остается прежним. Обязательно покажите это на самой сетке в соответствующих графах

Благодаря этому ребенку проще будет запомнить это правило, называемое коммутативным или переместительным. К тому же, так он быстрее запомнит определенные действия умножения и их произведения.

Это первые шаги, применяя которые вы положите начало запоминанию и к тому, чтобы быстро и просто потом выучить действия и результаты, указанные в сетке.

как выучить таблицу умножения

Подготовка к изучению таблицы умножения

Этот этап является в том числе организационным, но он входит в алгоритм того, как быстро и просто выучить таблицу умножения. Подготовка включает в себя такие шаги:

• Подберите время, когда вы ежедневно будете заниматься с ребенком. Учитывайте, что на изучение нужно уделять не менее 30 минут (это длительность одного занятия). Поэтому в это время ученик не должен быть уставшим, но должен быть готов к эффективному обучению;
• Приготовьтесь к тому, что процесс этот должен включать игровой момент, потому что так ученику гораздо проще запомнится этот материал;
• Саму сетку или столбики с примерами вы можете распечатать, а можете расчертить самостоятельно;
• Продумайте, как и когда, в какое время вы будете проверять выученный материал.

Основные принципы диеты 4

Прежде чем переходить к разговору о разрешенных и запрещенных продуктах, необходимо усвоить несколько основных правил:

1. Питание должно быть дробным. Пищу принимают 4-5 раз в день небольшими порциями.

2. Суточная калорийность рациона составляет примерно 2000 ккал. В случае сильной диареи и угрозы истощения эти цифры могут быть увеличены до 3000 ккал.

3. Строго ограничивается употребление овощей и фруктов, богатых клетчаткой, так как они способствуют развитию воспалительных процессов и вызывают брожение в кишечнике.

4. Обязательно соблюдение питьевого режима, чтобы предотвратить обезвоживание на фоне продолжительного расстройства стула (1,5 л в сутки).

5. Во избежание травматизации слизистой желудка необходимо следовать трем принципам щажения: термическому, механическому и химическому. Это означает, что ежедневное меню должно состоять из перетертых или жидких блюд комфортной температуры с полным исключением продуктов, имеющих резкий вкус (острое, кислое, копченое и т.д.). Предпочтительные способы приготовления – на пару, варка и тушение.

6. Из рациона исключают молоко. Каши варят только на воде.

7. Для супов используют овощные или некрепкие мясные бульоны.

8. Предпочтение лучше отдавать мясным блюдам из фарша.

9. Овощи подаются термически обработанными в виде пюре или в составе супов.

Диета 4: таблица разрешенных и запрещенных продуктов

ПРОДУКТ	РАЗРЕШЕНО	ЗАПРЕЩЕНО
Яйца	Не более 2 шт. в день	Сваренные вкрутую, яичница
Рыба	Хек, треска, минтай	Жареная с кожей, кляр, консервы
Мясо, птица	Курица, говядина, индейка, кролик, печень	Жирные сорта, баранина, дичь, копчености
Хлеб и выпечка	Подсушенный или вчерашний белый хлеб	Изделия из ржаной муки, слоеное тесто, свежая сдоба, блины
Молочные продукты	Некислый творог, сыр нейтрального вкуса с пониженным содержанием жира	Молоко, кисломолочные продукты
Крупы	Овсянка, манка, гречка, рис желательно в сильно разваренном виде	Бобовые, пшено
Овощи	В виде пюре после термической обработки	Чеснок, лук, грибы, горошек, в сыром виде
Фрукты и ягоды	Некислые сорта, обработанные термически	Сухофрукты, кислые разновидности
Напитки	Чай, отвар шиповника, кофе, разбавленные водой соки и компоты	Газировка, напитки с добавлением молока

Примерный рацион на день может выглядеть следующим образом:

Завтрак: Овсяная каша на воде с кусочком сливочного масла + сухарик из белого хлеба

Второй завтрак: пюре из запеченного яблока

Обед: Овощной суп-пюре + паровая котлета с гарниром из перетертой гречки

Полдник: Кисель

Ужин: Паровой омлет

pixabay.com &nbsp/&nbsp

Важно! Любая диета должная назначаться лечащим врачом. Стол №4 и его разновидности – не исключение

Перед тем, как выбирать ту или иную систему питания, обязательно посоветуйтесь со специалистом.

Учить таблицу деления – игра

Математическим действием, которое противоположно умножению, называется деление. Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.

Превращаем 100 примеров в 36

Таблица умножения на обратной стороне большинства тетрадок выглядит так:

На то, чтобы её выучить, может уйти целое лето. Понятно, что механическое заучивание правильных ответов к сотне примеров — самый трудоёмкий способ запомнить результаты умножения чисел до 10 друг на друга.

Процесс в разы ускоряется, когда мы показываем, как все эти 100 сочетаний можно сократить до 36. В этом деле куда более удачным наглядным пособием служит таблица Пифагора:

На её примере уже можно показать принципы умножения через площади небольших прямоугольников:

• 3 * 5 = 15, потому что в прямоугольник со сторонами длиной 3 и 5 клеточек помещается 15 маленьких квадратиков (считаем их вместе, чтобы убедиться).

• 5 * 3 = 15 по той же причине (считаем вместе).

Здесь же наглядно демонстрируем свойство коммутативности: от перестановки мест множителей произведение не меняется. Разумеется, название этого свойства лучше придержать до Хеллоуина, чтобы не пугать никого раньше времени

Из-за этого таблица Пифагора симметрична относительно своей диагонали, поэтому из 100 примеров для запоминания остаётся уже 55: сама диагональ с значениями 1, 4, 9, …, 100 и всё, что находится выше или ниже.

Это открытие можно сделать самостоятельно, заполнив часть пустой таблицы Пифагора, в которой изначально отмечены только множители:

Ребёнок может начать заполнять её, даже если ещё не знает правил умножения — складывать ведь он уже умеет, поэтому без труда посчитает сначала 2 + 2, потом 4 + 2, потом 6 + 2, и так, вплоть до 20. Потом ряд с тройками, и так далее.

Заполнив только часть таблицы (например, квадрат 6 * 6 клеток), уже можно увидеть одинаковые числа и понять, что зубрить её целиком совсем не нужно.

После этого на той же таблице Пифагора демонстрируем два принципа, позволяющие «автоматизировать» ещё 19 операций на умножение: умножение на 1 и умножение на 10:

• Если число умножить на единицу, оно никак не меняется.

• Если число умножить на 10, у него появляется ноль на конце.

Отнимаем от оставшихся ранее 55 примеров на умножение ещё 19 «автоматизированных» и получаем всего 36 сочетаний, которые нужно запомнить. Почти втрое меньше, чем предлагают нам на обложках тетрадок!

Уже легче, не так ли?

Степени

Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:

2 × 2 = 4,    3 × 3 = 9.

Квадраты. Произведение двух равных множителей называется квадратом числа.

В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.

Кубы. Произведение трех равных множителей называется кубом числа.

Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.

Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.

Произведения двух равных множителей или квадраты называются вторыми степенями.

Произведения трех равных множителей или кубы называются третьими степенями, и т. д.

Вы здесь

Таблица умножения и деления

Файлы: 

Вложение	Размер
Таблица умножения и деления, картинка с пояснением	74.46 КБ
Таблица умножения и деления	105.44 КБ
Таблица умножения и деления без ответов	19.53 КБ

Чтобы скачать и рапсечатать таблицу умножения и деления, используйте ссылки выше или нажмите правую кнопку мышки над картинками ниже и выберите «сохранить картинку как».

Таблица умножения и деления без ответов.

Тип:

материал

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Полезные советы

1. Ни в коем случае не ругайте ребенка, которому тяжело дается изучение таблицы умножения. Не позволяйте себе нервничать. Попытайтесь правильно мотивировать малыша и найти подходящую форму обучения. Изучение таблицы при помощи игр дает лучший результат, чем зубрежка.
2. Не налегайте и не требуйте слишком многого в короткие сроки. Лучше разделите нагрузку, чтобы процесс обучения не угнетал ребенка и не вызывал негативные эмоции. Делайте перерывы.
3. Развесьте дома плакаты, они подсознательно будут запоминаться. Делайте обучения красочным, веселым, игровым, а не нудным делом, которым больше никто в доме не занимается, «одного меня заставляют».
4. Снова и снова повторяйте пройденный материал, чтобы ребенок постоянно практиковался. Чередуйте методики, чтобы тема не приедалась.
5. Не ставьте в пример других детей и не стыдите ребенка. У всех разные способности. Каждый человек талантлив в своей сфере, и это необязательно математика.
6. Поощряйте ребенка приятными мелочами: деньгами на мороженое, маленькими подарочками, разрешением лечь спать на час позже, чтобы успеть посмотреть любимый мультик.

Умножение многозначного числа на однозначное

Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.

При этом ход вычислений выражают словесно:

1. Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).

2. Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.

3. Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.

4. Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.

Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:

1. Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.

2. Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.

3. Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.

4. Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.

5. Умножение продолжается до тех пор, пока не получат полного произведения.

Простые способы обучения детей таблице умножения

Девизом современной педагогики можно считать фразу «обучение с увлечением». Действительно, сегодня и на уроках, и на занятиях дома приветствуется использование игровых методик, интерактивных материалов.

Старый добрый счетный материал, а также разнообразные «подсказки» в виде стишков, песенок и интересных запоминающихся картинок тоже никто не отменял.

Имея представление об основных методиках обучения: запоминание, игра, визуализация – родители в силах самостоятельно научить ребенка таблице умножения.

Запоминание

Задача «выучить таблицу» предполагает в том числе ее буквальное запоминание. Подмечено, что запоминать материал куда легче в стихотворной форме или в виде песенки, особенно если дело касается детей.

Если упорядочить и зарифмовать примеры на умножение, то все нужные числа действительно гораздо быстрее закрепятся в памяти.

Использовать можно любые стихи (к примеру, можно выучить вместе с ребенком слова песни В. Шаинского и М. Пляцковского «Дважды два – четыре»). А родители с фантазией могут подключить ее и придумать свои рифмовки, это легко, например: «шестью семь – сорок два, прилетела к нам сова».

На крайний случай, если таблица уж никак не запоминается, остается рутинный, но проверенный не одним поколением школьников способ – вызубрить ее. Однако имейте в виду, что этот метод детишкам совсем не нравится.

Следует помнить, что запоминание не может быть единственным методом обучения ребенка таблице умножения

Важно не только запомнить последовательность чисел, но и понять суть самого действия. Именно это поможет ребенку в старшем возрасте решать сложные примеры на умножение

Визуализация

Еще одним способом освоения таблицы Пифагора является ее визуализация, предполагающая использование всевозможных наглядных материалов.

Это могут быть:

• счетные материалы;
• картинки;
• и даже пальцы!

С помощью счетного материала, будь то палочки, геометрические фигурки или что-то другое, можно показать ребенку суть умножения («6 х 5» означает «взять 6 раз по 5 предметов»).

Вдобавок, малыш может сосчитать представленные фигурки и убедиться, что ответ получился именно такой, как в таблице Пифагора.

С помощью картинок

Если ребенок любит рисовать – это отличный повод изучить таблицу с помощью картинок.

Принцип действия примерно такой же, как и в случае со счетным материалом, только вместо того, чтоб выложить перед юным математиком 6 раз по 5 палочек можно нарисовать прямо напротив примера 6 квадратов/тортиков/вагонов с 5 точечками/вишенками/зайчиками внутри каждого.

Правда, отрисовывать целые картины при умножении больших чисел будет сложновато.

На пальцах

Хорошим вариантом станет изучение части таблицы Пифагора, а именно столбца с девяткой, на пальцах. Такой своеобразный лайфхак заинтересует любого ребенка.

Расположите кисти рук перед собой ладонями наружу и пронумеруйте их мысленно от 1 до 10, начиная с левого мизинца. Табличные примеры на умножение с числом 9 решаются очень просто: достаточно загнуть палец, номер которого совпадает со вторым множителем.

Так, умножая 3 на 9, загибаем средний палец на левой руке. Пальцы, которые располагаются до загнутого (их два), обозначают количество десятков, а остальные (их семь) – количество единиц.

Итого, в ответе получаем 27. Быстро, легко и интересно!

Посредством обучающих мультфильмов и программ

В качестве средств визуализации, разумеется, можно привлекать обучающие мультфильмы, приложения на мобильных устройствах и программы на ПК, если есть такая возможность и родители не против подобного времяпрепровождения ребенка.

Конечно, для изучения такой непокорной таблицы умножения все средства хороши, но помните, что всего должно быть в меру, и не бросайте малыша на попечение гаджета в этом нелегком деле, а лучше присоединитесь к нему сами.

Игра

Обучение в игровой форме всегда привлекает малышей. Учить таблицу умножения хорошо на материале карточной игры. Из картона делаются карточки на каждый пример таблицы, на одной стороне пишется числовое выражение (5 х 3 = ?), а на другой – ответ.

Игроки по очереди вытягивают карточки, решают пример и проверяют себя, заглянув на обратную сторону. Если ответ правильный, карточка остается у игрока, если нет – возвращается в колоду. Победителем оказывается тот, у кого в конце игры наберется больше всего карточек.