Калькулятор онлайн

Вычитание

Вычитание это процесс переноса числа по числовой прямой влево, то есть против движения числовой прямой. При этом результаты вычитания могут быть различны: может получиться ноль, положительное или отрицательное число.

Несмотря на то, что результаты вычисления могут быть различны, результат всегда остается в категории действительных чисел или комплексных чисел, в зависимости от того, какие числа участвовали в вычислении. При вычитании рациональных чисел никогда не получится иррациональное число, а при вычитании действительных – комплексное. Нужно внимательно следить за этим.

Вычитать столбиком можно только рациональные числа с любым знаком. Столбиком не получится подсчитать вычитание обычных дробей, но эта операция всегда представляется в виде вычитания целых чисел в числителе, поэтому таким способом можно вычислять и подобные выражения.

Навигация по записям

Второй пример вычитания столбиком

Первый пример был очень простым, потому, что все цифры второго числа были меньше чем верхние…

Давайте возьмем другое число и попытаемся отнять столбиком…

Нам потребуется занимать десятки…

Давайте отнимем от 8345 число 978.

Первый пример был очень простым, потому, что все цифры второго числа были меньше чем верхние…

Давайте возьмем другое число и попытаемся отнять столбиком…

Нам потребуется занимать десятки…

Давайте отнимем от 8345 число 978.

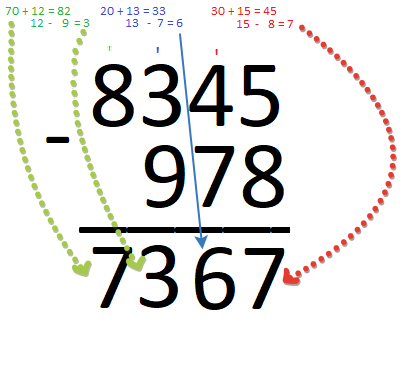
Опять выграниваем по правому краю.

Здесь существует правило! Если в одном столбце верхняя цифра меньше нижней, то нужно занимать единицу у следующей слева цифры.

Красным цветом…

Отнять от 5 8 не получится. Поэтому нужно занять единицу от 4 ставим апостроф над цифрой 4 – это означает, что там уже не 4, а на единицу меньше… 3

Чтобы понять, что это значит, то возьмите число 45 и представьте ё в виде 45 = 30 + 15

30 – это первая цифра(3) этого числа = 4 с апострофом и от 15 вычитаем 8 = 7 – опускаем за черту…

Синим цветом

4 с апострофом = 3 от неё надо вычесть 7 – повторятся аналогичная ситуация, что и первом случае…

Ставим апостроф над 3 , забираем оттуда десяток, у нас получилось 13 – 7 = 8 – опускаем за черту…

Зеленым цветом

Вместо 83 у нас 82, можно отнять так же столбиком, а можно и так… в уме 82 – 9 = 73

Опять выграниваем по правому краю.

Здесь существует правило! Если в одном столбце верхняя цифра меньше нижней, то нужно занимать единицу у следующей слева цифры.

Красным цветом…

Отнять от 5 8 не получится. Поэтому нужно занять единицу от 4 ставим апостроф над цифрой 4 – это означает, что там уже не 4, а на единицу меньше… 3

Чтобы понять, что это значит, то возьмите число 45 и представьте ё в виде 45 = 30 + 15

30 – это первая цифра(3) этого числа = 4 с апострофом и от 15 вычитаем 8 = 7 – опускаем за черту…

Синим цветом

4 с апострофом = 3 от неё надо вычесть 7 – повторятся аналогичная ситуация, что и первом случае…

Ставим апостроф над 3 , забираем оттуда десяток, у нас получилось 13 – 7 = 8 – опускаем за черту…

Зеленым цветом

Вместо 83 у нас 82, можно отнять так же столбиком, а можно и так… в уме 82 – 9 = 73

Вычитание в столбик однозначных объяснение для ребенка.

В качестве примера вычтем из 9 чилло 5. Если ребенок не умеет считать вообще, то можно показать на пальцах(ну по крайней мере нас учили так!). Не обязательно рассказывать и показывать на пальцах. Но почему это будет легче объяснить на пальцах, потому, что будет возникать визуальный ряд! Я не говорю, что такая методика правильная или не правильная — она просто существует и я её вам рассказываю! Это уже ваше дело какую методику выбирать!

Т.е. показываем ребенку 9 пальцев:

Убираем одну руку, которая обозначает 5 пальцев.

Спрашиваем у ребенка, сколько остается.

Проделываем так несколько раз, на разных числах.

Разбор примеров на деление столбиком на двузначное число

Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.

Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.

Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.

Значение частного чисел 265 и 53 равно 5.

Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

В частном будет однозначное число. 

Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.

Значение частного чисел 184 и 23 равно 8.

Рассмотрим более сложные случаи деления.

Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.

Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.

Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.

 Значение частного чисел 768 и 24 равно 32.

Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.

Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.

Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое  414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.

Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.

Значение частного чисел 15344 и 56 равно 274.

Деление на двузначное число с остатком

Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.

Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?

А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.

272 : 98    495 : 46    385 : 65   321 : 47

Проверь себя.

Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример

495 : 46

Почему в частном появился 0 (нуль)?

Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.

35 делим на  46. Берем по 0 (35 меньше, чем 46).  Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.

Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?

Давайте вместе решим эту задачу.

430 разделим на 35. Сделаем это столбиком (уголком).

Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.

Разделить можно на черновике, а решение в тетради записать в строчку.

430 : 35 = 12 (ост.10) – башен можно сделать.

Ответ: 12 башен и 10 деталей останется.

Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:

Решите самостоятельно практическую задачу.

Задача

Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?

Проверь себя.

Примеры вычитания в столбик

Пример 1

Отнимем 25 из числа 68.

Пример 2

Вычислим разность чисел: 35 и 17.

Пояснение:

Так как из цифры 5 нельзя отнять 7, мы занимаем один десяток у старшего разряда. Получается 5+10=15, а 15-7=8. И не забываем вычесть занятый десяток из соответствующего разряда, т.е. 3-1=2-1=1.

Пример 3

Вычтем число 46 из 70.

Пояснение:

Т.к. из нуля нельзя вычесть 6, занимаем один десяток. Следовательно, 0+10=10, а 10-6=4. Затем учитываем занятый десяток по выполнении вычитания в следующем разряде, т.е. 7-4-1=2.

Пример 4

Найдем разность двузначного и трехзначного чисел: 182 и 96.

Пояснение:

Из цифры 2 вычесть 6 не получится, значит занимаем один десяток. Получаем 2+10=12, 12-6=6. В десятках остается 8-1=7, но из 7 тоже нельзя отнять 9, значит занимаем десяток у сотен: 7+10=17, 17-9=8. Таким образом, в самих сотнях ничего не остается, т.к. 1-1=0.

Пример 5

Отнимем из 1465 числа 357, 214 и 78.

Пояснение:

В данном случае выполняем те же самые действия, что и в предыдущих примерах. Разница лишь в том, что при вычитании в столбце с единицами требуется занять не один, а два сразу десятка, т.е. 5+20=25, 25-7-4-8=6. В разряде десяток при этом останется 4 (6-2).

Вычитание столбиком из чисел, содержащих нули.

Опять же, разберем на примере:

Записываем числа в столбик. Которое больше — сверху. Начинаем вычитание справа налево по одной цифре. 9 — 3 = 6.

Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.

Обратите внимание: когда в вычитании столбиком над 0 есть точка, нуль становится девяткой. Над нашим нулем есть точка, значит, он стал девяткой

Вычитаем из нее 4. 9 — 4 = 5. Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0. Полученный нуль не нужно записывать

Над нашим нулем есть точка, значит, он стал девяткой. Вычитаем из нее 4. 9 — 4 = 5. Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0. Полученный нуль не нужно записывать.

Как вычитать столбиком

Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков – десятки и т. д. Результат вычитания записывают под чертой:

Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:

От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:

В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:

Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:

При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 – получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .

Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:

Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:

Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:

В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:

Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:

А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:

Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.

Вычитание столбиком подробное описание

Располагаем наши два числа, которые должны вычесть столбцом, по правилам, правая цифра под правой цифрой:

Смотрим первый столбец справа — 5 минус 4 — стандартная операция вычитания из большего числа меньшее, равно 1.

Второй столбец — 4 минус 9. 4 меньше 9, поэтому, забираем десяток из соседнего левого столбца(3) там остается 2.

Оставляем зарубку ‘ над числом 3, чтобы не забыть, что мы взяли оттуда единицу!

К десяти прибавляем 4 = 14, теперь мы можем отнять от 14 цифру 9 = 5 — сносим под черту.

Переходим к третьему столбцу справа. Это 3, но мы поставили там зарубку, что мы отсюда забрали единицу, значит здесь у нас осталась только двойка, 2 -1 = 1, сносим единицу под черту.

И последний столбец, под цифрой 8 ничего нет, и мы у восьмерки ничего не занимали, поэтому сносим её под черту без изменений.

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

3. Выполняем операцию вычитания  и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

Ответ: 1006005

Уравнение. Решение уравнений методом подбора

Ребята, внимательно посмотрите на карточки с цифрами трех поросят. Чья карточка подходит для записи в рамке? Почему?

Подходит карточка с цифрой 8, потому что 8 + 2 = 10.

Вместо окошка запишем латинскую букву х (икс).

Получится запись: х + 2 = 10.

Это уравнение.

Ниф-Ниф просит из чисел 6, 5, 2, 1 подобрать для каждого уравнения такое значение у (игрек), при котором получится верное равенство:

8 + у = 9                12 – у= 10                у + 7 = 12                 у – 5 = 1

Мы решили уравнения методом подбора. Обязательно нужно сделать проверку. Для этого вместо у (игрек) подставим в уравнение нужное число и убедимся, что равенство верное.

8 + у = 9 у = 1 8 + 1 = 9 9 = 9

у + 7 = 12 у = 5 5+7=12 12 = 12

12 – у = 10 у = 2 12 – 2 = 10 10 = 10

у – 5 = 1 у = 6 6 – 5 = 1 1 = 1

А теперь задание от Наф-Нафа. Ребята, найдите среди этих записей уравнение и решите его методом подбора.

3 + у             10 – х               14 – 2               b < 3               у – 6 = 2               а + 5

у – 6 = 2

у = 8

8 – 6 = 2

2 = 2

Сложение двух чисел в столбик: что нужно знать?

Прежде чем мы перейдем непосредственно к операции сложения в столбик, рассмотрим некоторые важные моменты. Для быстрого освоения материала желательно:

1. Знать и хорошо ориентироваться в таблице сложения. Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.
2. Помнить свойства сложения натуральных чисел. Особенно свойства, связанные со сложением нулей. Напомним их кратко. Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому. Сумма двух нулей есть нуль.
3. Знать правила сравнения натуральных чисел. 
4. Знать, что такое разряд натурального числа. Напомним, что разряд — это позиция и значение цифры в записи числа. Разряд определяет значение цифры в числе — единицы, десятки, сотни, тысячи и т.д.

Как научить собаку команде «Сидеть»

Классическое обучение данной команды выглядит следующим образом. В руку берется лакомство, показывается питомцу, но не дается. Рука с лакомством заносится над головой собаки, подается команда «Сидеть», одновременно другая рука надавливает на крестец собаки, принуждая собаку сесть. Как только она сядет, лакомство тут же отдается, следует бурная похвала с повтором команады.

В настоящее время кинологи предпочитают использовать бесконтактный вариант обучения данной команде. То есть, надавливания на крестец не производится, одновременно с произнесением команды «Сидеть», рука с лакомством заносится над головой и подается чуть вперед таким образом, чтобы собака была вынуждена запрокидывать ее назад, не отрывая взгляда от лакомства. В такой позиции для собаки будет естественно сесть, что она и сделает. Тут же нужно отдать лакомство и похвалить питомца.

Сложение столбиком

Сложение многозначных натуральных чисел удобней выполнять в столбик.

Сложение столбиком — это форма записи и способ сложения, используемый при сложении многозначных чисел. Сложение столбиком иначе ещё называют сложением в столбик.

Рассмотрим сложение столбиком на примере сложения чисел  7056  и  483.

Сложение в столбик записывается так: одно слагаемое записывается под другим так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства обычно меньшее число записывают под большим. Слева между слагаемыми ставится знак плюс, а под нижним слагаемым проводится горизонтальная черта:

Полученную запись можно мысленно разбить на столбики так, как это показано на рисунке:

Все дальнейшие действия сводятся к сложению однозначных чисел, которые находятся в одном столбике. Вычисление выполняется поразрядно справа налево, начиная с разряда единиц.

Если в результате сложения получается число меньшее  10,  то оно записывается под чертой в этом же разряде.

Начинаем вычисление с разряда единиц: складываем числа  6  и  3.  В результате имеем число  9.  Так как  9 < 10,  то записываем это число под чертой, в том же разряде:

Если в результате сложения получается число, равное  10  или большее  10,  то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа запоминается (оно используется на следующем шаге).

Переходим к сложению чисел в следующем разряде, то есть к сложению значений разряда десятков. Складываем числа  5  и  8,  получаем число  13.  Так как  13 > 10,  то под чертой, в том же разряде, записываем число  3  (это значение разряда единиц числа  13),  а число  1  запоминаем (это значение разряда десятков числа  13),  при этом говорят  три пишем, а один в уме.  Чтобы не забыть о запомненном числе, его обычно записывают сверху над следующим (слева) разрядом:

Запомненное число прибавляется к сумме чисел следующего разряда.

Переходим к следующему разряду и складываем числа  0  и  4.  В результате имеем  4.  К полученному числу прибавляем запомненное число  1,  получаем  5.  Так как  5 < 10,  то под чертой, в том же разряде, записываем число  5:

После этого происходит переход на один разряд влево и действия повторяются. Данный процесс продолжается до тех пор, пока числа не закончатся.

Если в столбике содержится только одно число, и у нас нет запомненного числа (от предыдущего сложения), в этом случае мы просто записываем это число под чертой, в том же разряде.

Так как в следующем столбике находится лишь одно число —  7,  и в памяти у нас нет запомненного числа, то мы просто записываем  7  под чертой, в том же разряде:

Дальше никаких чисел нет и в памяти тоже чисел нет. На этом процесс сложения можно считать завершённым. Натуральное число, получившееся под чертой, является результатом сложения данных чисел. Теперь можно записать сумму данных чисел в обычном виде:

7056 + 483 = 7539.

Рассмотрим ещё пару примеров сложения столбиком, чтобы разобраться с оставшимися нюансами.

Пример 1. Сложим числа  29  и  6  столбиком.

Складываем  9  и  6,  в результате получаем число  15.  Так как  15 > 10,  то число  5  записываем, а число  1  запоминаем:

Если в столбике содержится только одно число, и у нас имеется запомненное число (от предыдущего сложения), то запомненное число просто прибавляется к этому одному числу.

В следующем столбике находится лишь одно число —  2.  Так как у нас в памяти имеется число  1,  то его нужно прибавить к  2.  В результате получаем число  3:

Дальше никаких чисел нет и запомненного числа тоже нет, следовательно, сложение столбиком завершено.

Пример 2. Сложим столбиком числа  43  и  94.

Складываем  3  и  4.  В результате имеем число  7.  Так как  7 < 10,  то записываем это число под чертой, в том же разряде:

Если в последнем разряде в результате сложения получается число, равное  10  или большее  10,  то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа записывается под чертой в следующий разряд.

В следующем разряде складываем числа  4  и  9,  получаем число  13.  Так как  13 > 10,  то под чертой, в том же разряде, записываем число  3,  а число  1  записываем под чертой в следующий разряд:

Дальше никаких чисел нет и в памяти числа тоже нет, следовательно, сложение в столбик завершено.

Удобство сложения в столбик заключается в том, что сложение многозначных натуральных чисел фактически сводится к сложению однозначных чисел и запись процесса сложения занимает меньше места.

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, с нулями, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

Деление многозначных натуральных чисел столбиком

Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4  остаются неизменными. 
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам  описанного выше алгоритма.

Рассмотрим применение алгоритма деления многозначных чисел на примере.

Пример 3. Деление натуральных чисел в столбик

Разделим 5562 на 206.

В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на , 1, 2, 3.. и получаем:

206·=<556; 206·1=206<556; 206·2=412<556; 206·3=618>556

618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2

Выполняем вычитание столбиком

В результате вычитания имеем число 144. Справа от результата под чертой записываем число  из соответствующего разряда делимого и получаем новое рабочее число — 1442.

Повторяем с  ним пункты 2-4. Получаем:

206·5=1030<1442; 206·6=1236<1442; 206·7=1442

Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.

Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания. 

Ответ: 27

В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.

Пример 5. Деление натуральных чисел в столбик

Разделим натуральное число 238079 на 34.

Ответ: 7002

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Сложение столбиком трех и более чисел. Что нужно знать?

Во первых, нужно усвоить всю информацию, уже изложенную в этой статье. Во вторых, также помним, что нули не влияют на результат сложения, и сколько бы не было в выражении слагаемых нулей, их сумма будет равна нулю.

Этапы сложения в столбик трех и более чисел аналогичны этапам из уже рассмотренных примеров с двумя числами. Обратимся к практике и поясним ход решения.

Пример 5. Сложение трех натуральных чисел столбиком

Сложим столбиком числа 274, 3082 и 201297.

Сначала делаем запись:

Начинаем с первого столбика, справа налево.

4+2+7=13; 13>10

3 пишем, 1 в уме. Переходим ко второму столбику.

7+8+9=24; 24+1=25; 25>10

5 пишем, 2 в уме. Переходим к третьему столбику.

2++2=4; 4+2=6; 6<10

6 пишем, и ничего не запоминаем. Переходим к четвертому столбику.

3+1=4; 4<10

4 пишем, и ничего не запоминаем. Переходим к пятому столбику. Пятый и шестой столбики содержат по одному числу, в уме с предыдущих шагов мы ничего не держим, поэтому просто переносим числа из последних двух столбиков под черту.

Ответ: 274+3082+201297=204653

Совет: при сложении трех и большего количества чисел в столбик, если вычисления выходят слишком громоздкими, бывает удобнее последовательно сложить два числа, затем еще два и так далее.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.